35 Bocoran Soal PK UTBK Pengetahuan Kuantitatif dan Jawabannya

tirto.id - Contoh soal pengetahuan kuantitatif dapat dibaca dan dicermati peserta Ujian Tertulis Berbasis Komputer (UTBK). Pendaftar seleksi bisa membaca contoh soal penalaran kuantitatif (PK) sebelum mengikuti ujian.

PK UTBK adalah salah satu materi yang diujiankan dalam Seleksi Nasional Berdasarkan Tes (SNBT). Adapun kemampuan kuantitatif merujuk pada kemampuan perhitungan angka seseorang.

Dilansir dari laman resmi SNPMB, materi pengetahuan kuantitatif mencakup ukuran perhitungan, pemecahan masalah, dan pengetahuan umum matematika. Singkatnya, pengetahuan kuantitatif menguji kemampuan berhitung pesertanya.

Kumpulan Bocoran Soal PK UTBK Pengetahuan Kuantitatif dan Jawaban

Contoh soal PK UTBK 2025 dapat dijadikan sebagai bahan pembelajaran oleh calon mahasiswa. Pembimbing tes dari bimbingan belajar formal maupun nonformal juga bisa memanfaatkannya sebagai bahan ajar.

Berikut ini kumpulan contoh soal penalaran kuantitatif UTBK.

1. Jika nilai minimum fungsi kuadrat –8, grafik fungsinya (-1,0) dan (3,0), maka ketika melalui (4,b) nilai b adalah...

A. 42

B. 21

C. 10

D. 5

E. 0

Jawaban: C

2. Bilangan kurang dari 6000 dengan empat angka a094. Jika dibagi 3 hanya tersisa 1, nilai a adalah...

A. 1

B. 2

C. 3

D. 4

E. 5

Jawaban: C

3. a094 yang kurang dari 6000 memiliki berapa faktor prima?

A. 2

B. 3

C. 4

D. 5

E. 6

Jawaban: C

4. a094 yang kurang dari 6000 punya berapa faktor positif?

A. 17

B. 16

C. 15

D. 14

E. 4

Jawaban: B

5. Berdasarkan data b, -7, 3, -5, pernyataan yang benar mencakup:

1) Rata-ratanya –5, seandainya b adalah –11.

2) Mediannya –6, seandainya b adalah –7.

3) Modusnya –5, seandainya b adalah –5.

4) Jangkauannya 3, seandainya b adalah –8.

A. Nomor 1, 2, dan 3

B. Nomor 1 dan 3

C. Nomor 2 dan 4

D. Nomor 4

E. Semua benar

Jawaban: A

6. Belah ketupat ABCD merupakann segi empat, maka...

A. Semua sisinya sama panjang

B. Hanya dua sisi sama panjang

C. Punya empat diagonal

D. Semua sisinya tidak sama

E. Tidak ada jawaban yang benar

Jawaban: A

7. Jika segitiga ABC berbentuk siku A – B = 60 derajat dan C = a derajat, maka hubungan P dan Q yang sesuai adalah...

A. Q = P

B. P > Q

C. Q > P

D. P = Q

E. Tidak dapat ditentukan

Jawaban: E

8. Garis G mempunyai persamaan (2x – y) + p (x + y) = P, sementara garis h (x – 4y) + 2 p (x +Y) = 3p. Seandainya G dan H sejajar, perhitungan –2p yaitu...

A. 7

B. 14

C. -7

D. -16

E. -14

Jawaban: E

9. Suku ke-n baris geometri punya tiga suku pertama (P + 3), (P – 2), dan (P –8). Maka suku kelimanya adalah...

A. 1/7.776

B. - 7.776/125

C. 1.296/25

D. -1296/25

E. 7.776/25

Jawaban: C

10. Produksi sepatu menghasilkan empat produk yang berbeda dengan jumlah 75, 50, 50, dan 25. Berapakah rata-rata hasilnya...

A. 25

B. 60

C. 30

D. 40

E. 50

Jawaban: E

11. Nilai bruto suatu produk kemasan adalah Rp50.000, sementara pajak ditetapkan senilai 5 persen. Berapa angka pembayaran netto produknya?

A. Rp55.000

B. Rp52.500

C. Rp49.500

D. Rp48.500

E. Rp60.000

Jawaban: B

12. Siswa kelas 12 B dengan 10 nilai teratas adalah 75, 80, 90, 77, 87, 85, 89, 79, 76, dan 92. Rata-ratanya adalah...

A. 79

B. 80

C. 81

D. 82

E. 83

Jawaban: E

13. KPK bilangan prima x dan y yaitu 14, namun x > y. Berapakah nilai 3x – y?

A. 18

B. 19

C. 13

D. 23

E. 21

Jawaban: B

14. Terdapat bilangan 1/6 dan 1/8. Untuk memeroleh angka rata-rata 1/6, diperlukan tambahan...

A. 5/24

B. 5/12

C. 1/4

D. 12/5

E. 24/5

Jawaban: A

15. Seandainya (2x –5) < 3, maka x berbilangan bulatnya adalah...

A. Hasil perkalian x yaitu 6.

B. Jumlah x yaitu 10.

C. HP adalah (1, 2, 3, 4).

D. Hasil jumlah x yaitu 15.

E. Semua jawaban di atas benar.

Jawaban: A

16. Perbandingan kopi dan gula 2 : 3, sementara hitungannya kopi 2 sendok makan dan x adalah 3 sendok gula. Persamaan yang tepat sesuai pernyataan itu adalah...

A. 2 = x

B. 2 > x

C. 2 < x

D. 2 = Gula

E. Kopi = Gula

Jawaban: C

17. Target kereta dari Jakarta ke Yogyakarta ditempuh selama 8 jam, sementara kereta itu hanya mampu sampai ke lokasi selama 10 jam dengan kecepatan 50 km/jam. Jika ingin mencapai target, kereta harus berkecepatan...

A. 62,50 km/jam

B. 65,25 km/jam

C. 60,50 km/jam

D. 70,50 km/jam

E. 70 km/jam

Jawaban: A

18. Seandainya suatu himpunan A diisi oleh bilangan-bilangan bulat berurutan, maka pernyataan yang tidak benar adalah...

A. Median = rata-rata

B. Rata-rata = 0

C. 0 sama dengan rata-rata

D. Median = modus

E. Tidak ada jawaban yang benar

Jawaban: D

19. Jika 1 < x < y < z, maka nilai yang sesuai yaitu...

A. z (y + 1)

B. z (x + 1)

C. z (x + y)

D. z (x + z)

E. y (x + z)

Jawaban: C

20. Dalam urutan 15, 16, 20, 29, x, dan y, maka nilai x dan y adalah...

A. 45 dan 70

B. 70 dan 45

C. 35 dan 45

D. 45 dan 35

E. 50 dan 75

Jawaban: A

21. Diketahui X₁ dan X₂ adalah akar-akar dari persamaan x² + 3aX - (9+a) = 0. Apabila X₁² ditambah X₂² hasilnya 29, berapa nilai a dengan a lebih 0...

A. 5

B. 4

C. 3

D. 2

E. 1

Jawaban: E. 1

22. Perhatikan pernyataan berikut.

(1) f(3x)=3+6x

(2) f(2) > 7

(3) f(0) = 5

(4) g-1(-2)=-7

Apabila diketahui rumus fungsi (gof)(x-1) = x + 2 dan f(x) = 2x + 3. Manakah pernyataan yang benar?

A. (1) dan (2)

B. (1) dan (3)

C. (1) dan (4)

D. (2), dan (3)

E. (2) dan (4)

Jawaban: C. (1) dan (4)

23. Sebuah persamaan kuadrat Y = 3x² + (m − 2)x + 3 diketahui memiliki akar-akar kembar dan m > 0. Berapa nilai m yang memenuhi dari persamaan kuadrat tersebut?

A. 4

B. 2

C. 3

D. 6

E. 8

Jawaban: E. 8

24. Perhatikan pernyataan berikut.

(1) U3 > 8

(2) Suku pertama adalah 3

(3) U7 = 26

Apabila diketahui suatu barisan aritmatika x -2, 6, 2x + 2, 14,... Manakah pernyataan yang benar...

A. (1) dan (2)

B. (1) dan (3)

C. (2) dan (3)

D. (2)

E. (1), (2), dan (3)

Jawaban: B

25. Diketahui rumus fungsi f(x) = 2x − 3 dan (g o f)(x) = 4x – 9. Berapa nilai g-1 apabila mengacu kedua rumus fungsi tersebut...

A. 0

B. 1

C. -1

D. 2

E. -2

Jawaban: B

26. Diketahui (fog)(x) = 4x-2 dan g(x) = 2x+5. Berapa nilai dari invers F(x)...

A. 2x-10

B. 2x-12

C. 2x+12

D. (x+12)/2

E. (x-12)/2

Jawaban: E

27. Diketahui F(x) = (2x+3)^1/3 – 2. Tentukan Invers dari F(x)....

A. 1/2 (x+2)³-3/2

B. 1/2 (x-2)³+3/2

C. 1/3 (x+2)³-3/2

D. 1/3 (x-2)³+3/2

E. (x+2)³-3/2

Jawaban: A

28. Diketahui rumus fungsi F(x) = (5x-1)/(2x+3). Tentukan invers dari F(x)...

A. 3x+1/2x-5

B. -3x+1/2x-5

C. 3x+1/2x+5

D. 3x-1/2x-5

E. -3x-1/2x-5

Jawaban: E

29. ²log (3x-1) = 3. Berapa nilai dari x...

A. 2

B. 3

C. 4

D. 5

E. 6

Jawaban: B

30. 4^x+3 = ³√8^x+3. Nilai x adalah....

A. -2

B. -3

C. -4

D. 2

E. 3

Jawaban: B

31. Segitiga ABC siku-siku dengan P = a dan Q = 80

A. Tidak dapat ditentukan hubungan P dan Q

B. Q>P

C. P=Q

D. P>Q

Jawaban: A

32. Diketahui tiga bilangan asli berbeda dan kurang dari 10 dipilih sekaligus secara acak. Lantas, dari empat pernyataan berikut, berapakah yang bernilai benar berdasarkan informasi di atas?

1) Peluang semua bilangan yang terpilih prima kurang dari 1/20

2) Peluang semua bilangan yang terpilih genap kurang dari 1/25

3) Peluang jumlah semua bilangan yang terpilih kurang dari 8 adalah 1/42

4) Peluang semua bilangan yang terpilih ganjil lebih dari 1/7

A. 0

B. 1

C. 2

D. 3

E. 4

Jawaban: E

33. Perhatikan barisan bilangan real 2, a, 8, ...

Apakah 16 adalah salah satu suku barisan di atas?

Untuk menjawab pertanyaan tersebut, putuskan apakah pernyataan (1) dan (2) berikut ini sudah cukup sebagai jawaban:

1) Barisan tersebut adalah barisan aritmetika

2) Barisan tersebut adalah barisan bilangan positif

A. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetap pernyataan (2) SAJA tidak cukup

B. Pernyataan (1) dan (2) cukup untuk menjawab pertanyaan, tetapi salah satu keduanya tidak cukup

C. Pernyataan (1) ataupun pernyataan (2) SAJA sudah cukup untuk menjawab pertanyaan

D. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan

E. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup

Jawaban: E

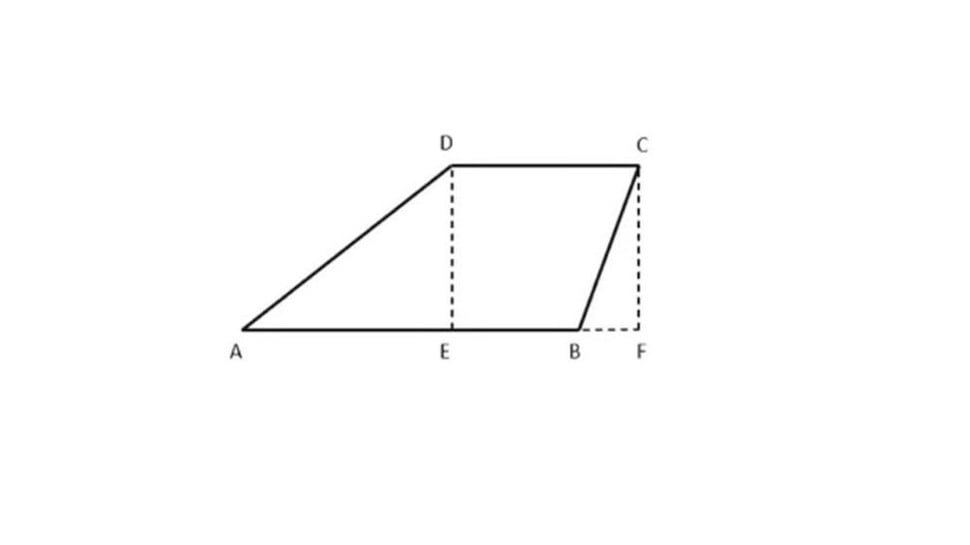
Gambar di bawah ini untuk soal nomor 34 dan 35!

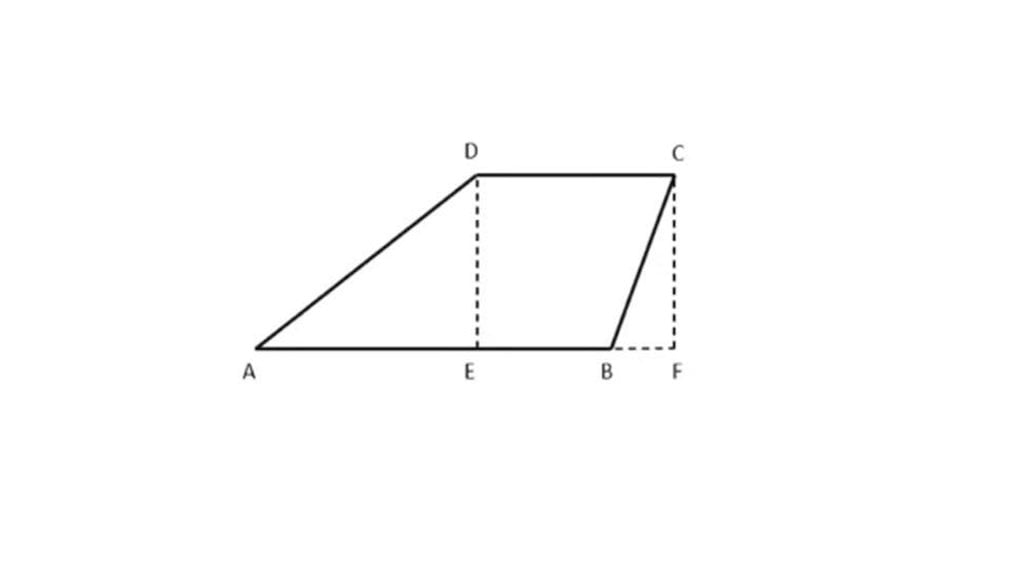
34. Pada trapesium ABCD dengan AB || CD, titik E dan F terletak pada garis AB sehingga DE tegak lurus AB dengan CF || DE. Maka, sudut ADC = ......

A. 100°

B. 135°

C. 105°

D. 120°

E. 145°

Jawaban: B

35. AE = ...

A. 2√3

B. 2√2

C. √2

D. 3

E. √3

Jawaban: A

Link Unduh Soal Pengetahuan Kuantitatif PDF

Contoh soal pengetahuan kuantitatif dapat ditemukan di laman resmi simulasi seleksi UTBK atau SNBT. Selain itu, Anda juga bisa mengunduh contoh soal pengetahuan kuantitatif PDF melalui laman berikut.

Link Download Soal Penalaran Kuantitatif UTBK PDF