Materi Kaidah Pencacahan Kelas 12 Kurikulum Merdeka

tirto.id - Rangkuman materi Kaidah Pencacahan kelas 12 Kurikulum Merdeka bisa dijadikan bahan referensi belajar bagi siswa agar dapat mengikuti seluruh proses pembelajaran mata pelajaran matematika dengan baik.

Mata pelajaran Matematika kelas 12 Kurikulum Merdeka terbagi menjadi beberapa bab yang membahas sejumlah persoalan matematika.

Salah satu bab tersebut akan mempelajari mengenai Kaidah Pencacahan. Pada bab tersebut Siswa akan belajar menghitung jumlah kemungkinan atau pola-pola tertentu dengan lebih sistematis.

Materi Matematika Kaidah Pencacahan, dijabarkan melalui serangkaian materi. Maka itu, dianjurkan bagi siswa untuk menyimak rangkuman materinya supaya dapat lebih mudah memahami dan memecahkan soal.

Rangkuman Materi Kaidah Pencacahan Kelas 12 Kurikulum Merdeka

Berikut ini adalah rangkuman materi Kaidah Pencacahan kelas 12 Kurikulum Merdeka yang bisa dijadikan bahan belajar serta bahan persiapan untuk mengikuti pembelajaran materi Matematika kelas 12.

Sebelum mengetahui berbagai materi dalam Kaidah Pencacahan, maka perlu diketahui apakah Kaidah Pencacahan itu sebenarnya.

I. Pengertian Kaidah Pencacahan

Kaidah Pencacahan adalah suatu ilmu dalam matematika yang bertujuan menentukan banyaknya cara suatu percobaan dapat terjadi, dengan cara penjumlahan atau perkalian.

Kaidah Pencacahan juga berfungsi untuk membantu siswa menghitung jumlah kemungkinan atau pola-pola tertentu dengan cara yang lebih sistematis. Kaidah Pencacahan bisa diterapkan di banyak kasus, mulai dari masalah kombinatorik, probabilitas, hingga statistik.

Singkatnya, Kaidah Pencacahan adalah cabang matematika yang membahas cara menghitung banyaknya susunan atau kombinasi suatu objek tanpa harus merinci semua kemungkinan susunannya.

II. Aturan Penjumlahan

Jika ada sebanyak a benda pada himpunan pertama dan ada sebanyak b benda pada himpunan kedua, dan kedua himpunan itu tidak beririsan, maka jumlah total anggota di kedua himpunan adalah a + b.

Contoh:

Jika seseorang akan membeli sebuah sepeda motor di sebuah dealer. Di dealer itu tersedia 5 jenis Honda, 3 jenis Yamaha, dan 2 jenis Suzuki. Dengan demikian orang tersebut mempunyai pilihan sebanyak 5 + 3 + 2 = 10 jenis sepeda motor.

Contoh:

Ibu Alya seorang guru SMK. Ia mengajar kelas XII Akuntansi yang jumlahnya 40 siswa, kelas XII penjualan yang jumlahnya 42 siswa, kelas XII bisnis, yang jumlahnya 45 siswa, maka jumlah siswa yang diajar Ibu Alya adalah 40 + 42 + 45 = 127 siswa.

III. Aturan Perkalian

Pada aturan perkalian ini dapat diperinci menjadi dua, namun keduanya saling melengkapi dan memperjelas. Kedua kaidah itu adalah menyebutkan kejadian satu persatu dan aturan pengisian tempat yang tersedia.

Contoh:

Misal himpunan celana A = {a1 ,a2 ,a3} dan himpunan baju B = {b1, b2}.

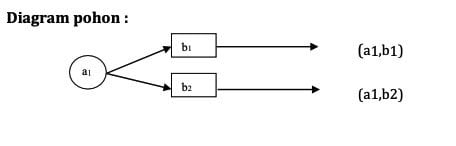
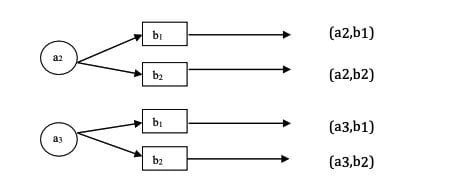
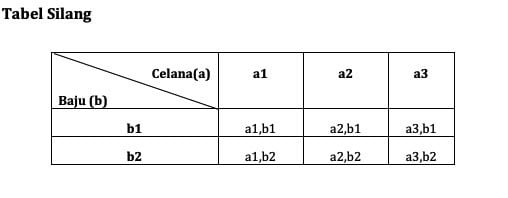
Pasangan berurutan

Himpunan pasangan terurut dari himpunan tersebut adalah {( a1,b1), (a2,b1), (a3,b1), (a1,b2), (a2,b2), (a3,b2)}. Jadi, terdapat 6 cara untuk memasangkan celana dan baju.

Contoh:

Misalkan dari Kota X ke Kota Y ada tiga jalan yang dapat dilalui dan dari Kota Y ke Kota Z ada lima jalan yang dapat dilalui. Tentukan banyaknya jalan yang mungkin dapat dilalui untuk bepergian dari Kota X ke Kota Z melalui Kota Y.

Jawaban:

Dari Kota X ke Kota Y ada 3 jalan dan dari Kota Y ke Kota Z ada 5 jalan.

Jadi, seluruhnya ada 3 x 5 = 15 jalan yang dapat dilalui.

Contoh:

Diberikan angka 0, 1, 2, 3, 4, 5 dan 7 akan dibentuk bilangan ribuan dan tidak boleh ada angka yang sama. Tentukan banyak bilangan yang kurang dari 4.000 yang dapat terjadi.

Jawaban:

Angka ribuan dapat dipilih dari 3 angka yang mungkin, yaitu 1, 2, dan 3.

Misalkan dipilih angka 1. Angka ratusan dapat dipilih dari 6 angka yang mungkin yaitu 0, 2, 3, 4, 5, dan 7. Misalkan dipilih angka 2. Angka puluhan dapat dipilih dari 5 angka yang mungkin, yaitu 0, 3, 4, 5, dan 7.

Misalkan dipilih angka 3. Angka satuan dapat dipilih dari 4 angka yang mungkin, yaitu 0, 4, 5, dan 7. Jadi banyak bilangan dapat terjadi adalah 3 x 6 x 5 x 4 = 360 bilangan.

IV. Faktorial

Untuk mempermudah perhitungan peluang suatu kejadian kita gunakan notasi faktorial. Faktorial dinotasikan dengan tanda seru “ ! “.

Faktorial merupakan penulisan singkat dari perkalian sederajat bilangan bulat positif terurut hingga 1.

Faktor dapat didefinisikan sebagai berikut :

Definisi:

n! = 1 × 2 × 3 × …× (n – 2) × (n – 1) × n atau

n! = n × (n – 1) × (n – 2) × … × 3 × 2 × 1

1! = 1 dan 0! = 1

Contoh:

1. 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720

2. 3! × 2 ! = 3 × 2 × 1 × 2 × 1 = 6 × 2 = 12

3. 10!/8! = 10x9x8!/8x = 10x9 =190

V. Permutasi

Permutasi merupakan salah satu kaidah pencacahan dalam matematika yang digunakan untuk menghitung banyaknya susunan terurut dari objek-objek yang berbeda.

Contohnya, jika ada n objek, permutasi akan menghitung berapa banyak cara untuk mengatur objek-objek tersebut dalam suatu urutan tertentu.

Dalam permutasi, setiap objek harus ditempatkan pada posisi yang berbeda-beda dalam susunan yang terurut.

nPr = n!/(n-r)!

Keterangan:

n = Jumlah objek yang tersedia

r = Jumlah objek yang akan diatur.

Dalam permutasi, urutan adalah hal yang penting, sehingga dua susunan yang berbeda dari objek yang sama dianggap sebagai susunan yang berbeda juga.

Contoh:

Pengaturan 4 buku pada rak buku. Jika ada 4 buku dan kita ingin menghitung berapa banyak cara untuk mengatur keempat buku tersebut, maka kita menggunakan rumus permutasi

Diketahui:

n=4

r=4

Jawab:

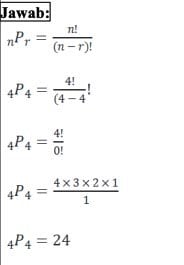
VI. Kombinasi

Kombinasi digunakan untuk menghitung banyaknya cara memilih objek-objek tertentu dari sekelompok objek tanpa memperhatikan urutan atau posisi objek tersebut.

Jadi, dengan kombinasi, kita dapat menghitung berapa banyak cara memilih objek-objek tersebut tanpa harus memperdulikan posisi atau urutannya. Rumus kombinasi sendiri berbeda dengan permutasi dan faktorial.

Rumus kombinasi menggunakan faktorial dan permutasi untuk menghitung jumlah cara memilih objek-objek tersebut.

Berikut rumus kombinasi peluang yang wajib diketahui:

nCr = n! / r!(n-r)!

Di mana n! menunjukkan faktorial dari n, yang dapat dihitung dengan mengalikan semua bilangan bulat positif dari 1 hingga n, dan r! dan (n-r)! masing-masing menunjukkan faktorial dari r dan n-r.

Contoh:

Jika terdapat 8 orang yang ingin dipilih dari 12 orang untuk membentuk sebuah tim, berapa banyak cara yang mungkin untuk memilih tim tersebut?

Diketahui:

n = 12 (jumlah total orang yang tersedia)

r = 8 (jumlah orang yang ingin dipilih untuk tim)

Jawaban:

Jadi, ada 495 cara yang mungkin untuk memilih tim dari 12 orang yang tersedia.

VII. Aturan Kaidah Pencacahan

1. Pencacahan Boleh Berulang

Aturan pencacahan berulang membolehkan untuk memilih objek yang sama lebih dari satu kali dan menempatkannya pada posisi yang berbeda dalam susunan yang dibuat. Sehingga objek yang sudah dipilih bisa dipilih lagi untuk ditempatkan pada posisi yang berbeda dalam susunan tersebut.

Contoh:

Berapa banyak kombinasi yang bisa kamu bikin dari 3 warna (merah, kuning, dan hijau) jika ingin membuat lampion menggunakan 6 kertas origami dan tiap kertas bisa diwarnai sama atau beda?

Jawaban:

Kita bisa menggunakan aturan pencacahan boleh berulang karena warna bisa dipakai berulang

kali. Jadi setiap kertas punya 3 pilihan warna. Maka total kombinasinya adalah:

3×3×3×3×3×3=729

Jadi ada 729 kombinasi yang bisa kita buat untuk bikin lampion pake 6 kertas origami dan 3 warna yang ada.

2. Pencacahan Tidak Boleh Berulang

Aturan ini membolehkan untuk memilih objek-objek yang berbeda untuk ditempatkan dalam suatu susunan, sehingga setiap objek hanya bisa dipilih satu kali saja dan tidak boleh dipilih kembali.

Misalnya, dalam memilih anggota tim, setiap orang hanya bisa dipilih satu kali dan tidak bisa dipilih kembali untuk menjadi anggota tim yang sama. Aturan ini juga sering digunakan dalam perhitungan peluang di mana hasil yang sama tidak dapat muncul kembali dalam percobaan yang sama.

Contoh:

Seorang siswa ingin memilih 4 buku dari rak buku di perpustakaan. Jika terdapat 10 buku yang berbeda di rak tersebut, berapa banyak cara siswa tersebut dapat memilih 4 buku tanpa memilih buku yang sama?

Jawaban:

Karena setiap buku hanya dapat dipilih sekali, maka kita menggunakan aturan pencacahan tidak boleh berulang. Kita dapat menghitung jumlah kombinasi dengan rumus:

Jadi, ada 210 cara siswa tersebut dapat memilih 4 buku tanpa memilih buku yang sama.