Rangkuman Materi Trigonometri Kelas 10 Kurikulum Merdeka

tirto.id - Rangkuman materi trigonometri kelas 10 Kurikulum Merdeka bisa menjadi bahan belajar sekaligus referensi siswa-siswi.

Trigonometri adalah salah satu bab yang dipelajari siswa kelas 10 untuk mata pelajaran matematika. Nantinya, siswa dapat menghitung sudut-sudut segitiga, sekaligus mengasah nalar dan logika mengenai bangun datar maupun bangun ruang.

Untuk lebih bisa memahami trigonometri, siswa kelas 10 dapat semakin giat mempelajari berbagai materi, termasuk berlatih soal trigonometri. Berikut ini penjelasan materi trigonometri siswa kelas 10 Kurikulum Merdeka.

Rangkuman Materi Trigonometri Kelas 10 Kurikulum Merdeka

Siswa yang mempelajari materi trigonometri bakal semakin sering bertemu dengan sejumlah istilah kunci, seperti sinus, tangen, cosecan, secan, cotangen, dan nilai perbandingan.

Trigonometri merupakan sebuah cabang matematika yang berhadapan dengan sudut segitiga. Contohnya sinus, cosinus, dan tangen.

Untuk semakin mendalami ilmu trigonometri, siswa perlu memahami identitas trigonometri dan nilai perbandingan dari suatu sudut. Konsep sudut berelasi dan pengukuran sudut termasuk hal yang penting.

Pengukuran sudut menjadi salah satu aspek krusial dalam pengukuran dan pemetaan kerangka maupun titik-titik detail. Sistem besaran sudut yang dipakai juga berbeda antara satu dengan yang lainnya.

Sistem besaran sudut pada pengukuran dan pemetaan terdiri dari:

• Sistem Besaran Sudut Seksagesimal

• Sistem Besaran Sudut Sentisimal

• Sistem Besaran Sudut Radian

Dasar mengukur besaran sudut seperti suatu lingkaran yang dibagi menjadi empat bagian dinamakan kuadran yaitu Kuadran I, II, III dan kuadran IV.

Untuk cara sexagesimal, lingkaran dapat dibagi menjadi 360 bagian yang sama dan tiap bagiannya disebut derajat. Maka, 1 kuadran dalam lingkaran tersebut = 900. Jadi, 1°= 60’ 1’ = 60” 1° = 3600”

Identitas Trigonometri

Identitas trigonometri adalah kesamaan yang memuat perbandingan trigonometri dari suatu sudut. Pada identitas trigonometri dikenal istilah sinus, cosinus, dan tangen. Ketiganya akan menjadi dasar dalam beberapa rumus matematika.

Bagaimana cara membuktikan identitas trigonometri? Sebuah identitas trigonometri dapat ditunjukkan kebenarannya dengan tiga cara.

• Pertama, dimulai dengan menyederhanakan ruas kiri menggunakan identitas sebelumnya sampai menjadi bentuk yang sama dengan ruas kanan.

• Kedua, mengubah dan menyederhanakan ruas kanan sampai menjadi bentuk yang sama dengan ruas kiri.

• Ketiga, mengubah baik ruas kiri maupun ruas kanan ke dalam bentuk yang sama.

Ada 3 rumus identitas trigonometri yang perlu diketahui. Di antaranya adalah sebagai berikut:

Rumus 1 dan 2:

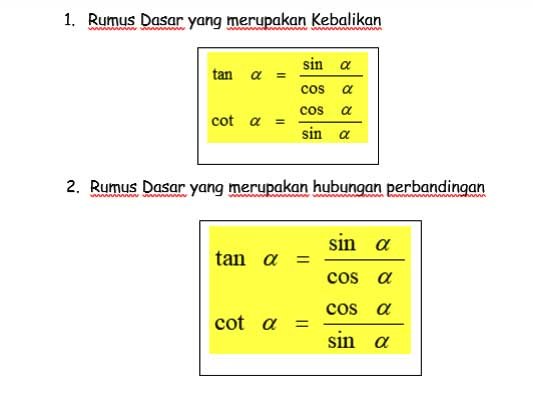
Rumus 3:

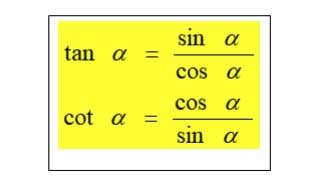
Perbandingan trigonometri pada segitiga siku-siku:

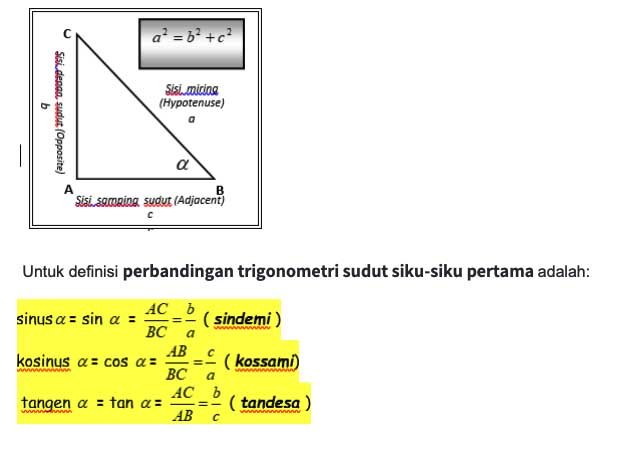
Dan untuk definisi perbandingan trigonometri sudut siku-siku kedua adalah:

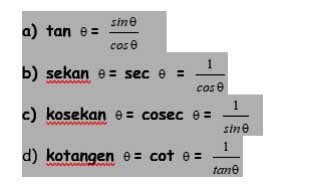
Perbandingan sudut dan sudut berelasi trigonometri I

Perbandingan sudut dan relasi trigonometri merupakan perluasan dari definisi dasar trigonometri tentang kesebangunan pada segitiga siku-siku. Hal ini hanya memenuhi sudut kuadran I dan sudut lancip (0 − 90°).

Berikut ini contohnya:

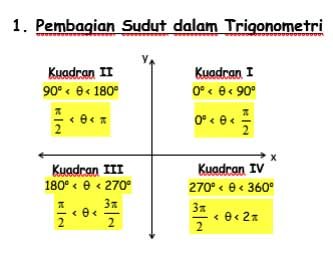
Perbandingan sudut dan sudut berelasi trigonometri II

Untuk setiap α lancip, maka (90° + α) dan (180° − α) akan menghasilkan sudut kuadran II. Dalam trigonometri, relasi sudut-sudut tersebut dinyatakan sebagai berikut: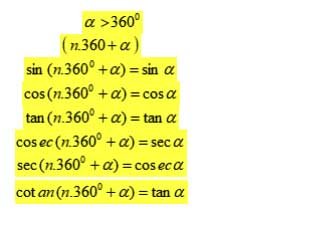

Fungsi Trigonometri

Fungsi trigonometri adalah suatu fungsi yang grafiknya berulang secara terus menerus dalam periode tertentu. Fungsi trigonometri terdiri atas bukit dan lembah yang berulang-ulang secara terus menerus dalam periode tertentu.

Unsur-unsur grafik trigonometri

Pada fungsi trigonometri terdapat beberapa unsur, yakni periode, amplitudo, nilai maksimum, dan nilai minimum.

a. Periode

Periode adalah jarak antara dua puncak atau dua lembah pada grafik fungsi trigonometri. Atau dapat diartikan juga sebagai jarak terjadinya grafik fungsi trigonometri tersebut berulang.

b. Amplitudo

Amplitudo adalah setengah dari selisih nilai maksimum dan minimum dari suatu fungsi.

c. Nilai Maksimum

Nilai maksimum adalah nilai tertinggi yang bisa dicapai oleh suatu fungsi trigonometri. Pada grafik, nilai maksimum merupakan titik puncak dari bukit.

d. Nilai Minimum

Nilai minimum adalah nilai terendah yang bisa dicapai oleh suatu fungsi trigonometri. Pada grafik, nilai minimum merupakan titik terendah dari lembah.

Jenis-jenis grafik fungsi trigonometri

Fungsi trigonometri sederhana terdiri dari tiga macam atau jenis, yaitu fungsi sinus, fungsi cosinus, dan fungsi tangen. Nah, masing-masing fungsi tersebut dapat dijelaskan menggunakan grafik baku fungsi trigonometri.

Contoh Soal Trigonometri

Berikut ini beberapa contoh soal trigonometri yang bisa dipelajari siswa kelas 10 Kurikulum Merdeka:

1. Tentukan nilai maksimum dan nilai minimum dari fungsi trigonometri di bawah in!

a. f(x) = 2 sin 2x + 5

b. f(x) = -3 cos (3(x+90°)) – 8

Penyelesaian:

a. f(x) = 2 sin 2x + 5 → a = 2 , c = 5

Nilai maksimum = |a| + c = |2| + 5 = 7

Nilai minimum = -|a| + c = -|2| + 5 = 3

b. f(x) = -3 cos (3(x+90°)) – 8

f(x) = – 3 cos (3x+270°) – 8 → a = -3 , c = -8

Nilai maksimum = |a| + c = |-3| + (-8) = 3 – 8 = -5

Nilai minimum = -|a| + c = -|-3| + (-8) = -3 – 8 = -11

2.

3.

Untuk melihat lebih banyak contoh soal trigonometri kelas 10 Kurikulum Merdeka, siswa dapat mengunjungi link berikut ini:

Contoh Soal Trigonometri Kelas 10 Kurikulum Merdeka