25 Contoh Soal PAT Matematika Kelas 8 Semester 2 dan Jawabannya

tirto.id - Kumpulan contoh soal PAT atau UAS Matematika kelas 8 semester 2 dan jawabannya ini dapat dijadikan bahan belajar bagi peserta didik yang akan mengikuti ujian sekolah Penilaian Akhir Tahun atau Ujian Akhir Semester.

PAT atau UAS adalah ujian sekolah untuk mengetahui sejauh mana peserta didik memahami berbagai materi pelajaran yang sudah diberikan di kelas hingga akhir semester berlangsung.

Salah satu materi PAT atau UAS kelas 8 adalah mata pelajaran Matematika. Agar siswa kelas 8 dapat mempersiapkan diri untuk mengikuti ujian sekolah dengan baik, berikut ini akan disampaikan kisi-kisi soal PAT atau UAS Matematika kelas 8, termasuk contoh soal dan kunci jawabannya.

Kisi-Kisi Soal UAS Matematika Kelas 8 Semester 2

Untuk mengingatkan siswa kelas 8 semester 2 terhadap berbagai materi Matematika yang sudah diajarkan, berikut ini kisi-kisi soal ujian akhir sekolah Matematika kelas 8 semester 2:

1. Menjelaskan dan membuktikan teorema Pythagoras dan tripel Pythagoras.

- Hubungan antar panjang sisi pada segitiga siku-siku

- Pemecahan masalah yang melibatkan teorema Pythagoras

2. Menjelaskan sudut pusat, sudut keliling, panjang busur, dan luas juring lingkaran, serta hubungannya.

- Lingkaran

- Unsur-unsur lingkaran

- Hubungan sudut pusat dengan sudut keliling

- Panjang busur

- Luas juring

- Garis singgung persekutuan dalam dua lingkaran

- Garis singgung persekutuan luar dua lingkaran

3. Menjelaskan garis singgung persekutuan luar dan persekutuan dalam dua lingkaran dan cara melukisnya.

- Lingkaran

- Unsur-unsur lingkaran

- Hubungan sudut pusat dengan sudut keliling

- Panjang busur

- Luas juring

- Garis singgung persekutuan dalam dua lingkaran

- Garis singgung persekutuan luar dua lingkaran

4. Membedakan dan menentukan luas permukaan dan volume bangun ruang sisi datar (kubus, balok, prisma dan limas).

- Kubus, balok, prisma dan limas

- Jaring-jaring : kubus, balok, prisma dan limas

- Luas permukaan : kubus, balok, prisma dan limas

- Volume : kubus, balok, prisma dan limas

- Menaksir volume bangun ruang tak beraturan

5. Menganalisis data berdasarkan distribusi data, nilai rata-rata, median, modus dan sebaran data untuk mengambil kesimpulan, membuat keputusan dan membuat prediksi.

- Rata-rata, median, dan modus

- Mengambil keputusan berdasarkan analisis data

- Membuat prediksi berdasarkan analisis data

6. Menjelaskan peluang empirik dan teoritik suatu kejadian dari suatu percobaan.

- Titik sampel

- Ruang sampel

- Kejadian

- Peluang empirik

- Peluang teoritik

- Hubungan antara peluang empirik dan peluang teoritik

Kumpulan Contoh Soal PAT Matematika Kelas 8 Semester 2 dan Jawabannya

Berikut ini adalah contoh soal penilaian akhir tahun atau ujian akhir semester Matematika kelas 8 semester 2 beserta jawabannya:

Soal Pilihan Ganda

1. Banyaknya titik sudut pada prisma segitiga adalah ....

A. 6 buah

B. 8 buah

C. 10 buah

D. 12 buah

Jawaban: A

2. Berikut ini merupakan ciri khusus dari limas, yaitu ....

A. memiliki titik puncak

B. memiliki dua sisi yang sama bentuk dan ukurannya

C. memiliki panjang rusuk yang sama

D. memiliki sisi berhadapan yang sama panjang

Jawaban: A

3. Banyaknya rusuk alas pada limas segi empat adalah ....

A. 3 buah

B. 4 buah

C. 7 buah

D. 8 buah

Jawaban: B

4. Panjang kawat yang dibutuhkan untuk membuat model kerangka kubus yang panjang rusuknya 18 cm adalah.....

A. 72 cm

B. 108 cm

C. 216 cm

D. 500 cm

Jawaban: C

5. Budi mempunyai kawat sepanjang 24 meter. Ia akan membuat kerangka balok yang berukuran 15 cm x 12 cm x 13 cm. Banyak kerangka balok yang dapat dibuat adalah ….

A. 10 buah

B. 12 buah

C. 13 buah

D. 15 buah

Jawaban: D

6. Volum kubus yang panjang rusuknya 8 cm adalah....

A. 384 cm3

B. 512 cm3

C. 616 cm3

D. 724 cm3

Jawaban: B

7. Sebuah balok memiliki ukuran panjang 15 cm, lebar 11 cm, dan tinggi 9 cm. Luas permukaan balok tersebut adalah ....

A. 798 cm²

B. 797 cm2

C. 796 cm²

D. 795 cm²

Jawaban: A

8. Volum balok yang berukuran panjang 20 cm, lebar 15 cm dan tinggi 10 cm adalah....

A. 1500 cm3

B. 1750 cm3

C. 1800 cm3

D. 3000 cm3

Jawaban: D

9. Luas permukaan prisma yang alasnya berbentuk segitiga siku-siku dengan sisi 12 cm, 16 cm dan 20 cm, dan tinggi prisma 25 cm adalah....

A.1200 cm2

B. 1392 cm2

C. 1400 cm2

D. 2400 cm2

Jawaban: D

10. Alas sebuah limas adalah sebuah segitiga dengan panjang alas 10 cm dan tinggi 18 cm. Jika tinggi limas tersebut adalah 18 cm maka volume limas adalah ....

A. 420 cm3

B. 540 cm3

C. 1.246 cm3

D. 1.200 cm3

Jawaban: B

11. Luas permukaan limas yang alasnya berbentuk persegi dengan panjang sisi 12 cm dan tinggi limas 8 cm adalah....

A. 384 cm2

B. 428 cm2

C. 480 cm2

D. 768 cm2

Jawaban: A

12. Sebuah kubus PQRS.TUVW memiliki panjang rusuk 13 cm. Panjang diagonal bidang kubus tersebut adalah...

A. akar 13 cm

B. 2 akar 13 cm

C. 13 akar 2 cm

D. 12 akar 2 cm

Jawaban: C

13. L merupakan luas lingkaran dan d diameter lingkaran, maka rumus luas lingkaran adalah....

A. L = 2π d

B. L = π d2

C. L = π d2

D. L = π d2

Jawaban: D

14. Jika diameter suatu lingkaran 3,5 m dan π = 22/7 , maka keliling lingkaran adalah ….

A. 11,5 m

B. 11 m

C. 10,5 m

D. 7,5 m

Jawaban: B

15. Sebuah sepeda memiliki roda berjari-jari 42 cm. Jika roda berputar sebanyak 2500 kali maka panjang lintasan lurus yang dilaluinya adalah....

A. 3,3 km

B. 6,6 km

C. 33 km

D. 66 km

Jawaban: A

16. Untuk membuat bingkai antena parabola digunakan plat aluminium sepanjang 2,64 m. Jika π = 22/7 , maka diameter antena parabola tersebut adalah ….

A. 96 cm

B. 84 cm

C. 72 cm

D. 64 cm

Jawaban: B

17. Sebuah lingkaran memiliki luas 616 cm² maka diameter lingkaran tersebut adalah ....

A. 7 cm

B. 14 cm

C. 21 cm

D. 28 cm

Jawaban: D

18. Di dalam lapangan rumput berbentuk persegi dengan sisi 6 m, terdapat taman bunga berbentuk lingkaran dengan diameter 4 m. Jika π = 3,14 , maka luas daerah yang ditumbuhi rumput adalah ….

A. 23,46 m2

B. 23,44 m2

C. 24,34 m2

D. 32,44 m2

Jawaban: B

19. Luas suatu lingkaran adalah 108 cm². Jika luas juring AOB pada lingkaran tersebut adalah 12 cm² maka besarnya sudut AOB adalah ....

A. 90°

B. 60°

C. 40°

D. 30°

Jawaban: C

20. Daerah pada lingkaran yang dibatasi oleh busur dan tali busur adalah....

A. juring lingkaran

B. busur lingkaran

C. tembereng

D. diameter lingkaran

Jawaban: C

Soal Uraian:

1. Suatu kolam renang mempunyai ukuran panjang 40 m dan lebar 15 m. Kedalaman air pada ujung yang paling dangkal 1,3 m dan ujung yang paling dalam 2,7 m. Berapa liter volume air dalam kolam renang tersebut?

Jawaban:

V kolam = {12a+bxt}xlebar kolam}

= {121,3+2,7x40}x15}

= 124,0xt}x600

= 2x 600

= 12.00 m3

= 12.000 liter

Jadi, volume air dalam kolam renang tersebut adalah 12.000 liter.

2. Dua lingkaran mempunyai jari-jari masing-masing 10 cm dan 3 cm. Jika jarak kedua titik pusat lingkaran 25 cm, hitunglah panjang garis singgung persekutuan luar kedua lingkaran tersebut!

Jawaban:

L2 = p2-(R+r)2

= 252-(10-3)2

= 252- 72

= 625-49

= 576

= 576

= 24

Jadi, panjang garis singgung persekutuan luarnya adalah 24 cm

3. Hitunglah keliling lingkaran yang berjari-jari 21 cm dengan π = !

Jawaban:

Keliling = 2πr

= 2x227x21

= 132 cm

Jadi, keliling lingkaran adalah 132 cm

4. Hitunglah luas seluruh permukaan kubus yang memiliki panjang rusuk 25 cm!

Jawaban:

Luas = 6 s2

= 6x252

= 6 x 625

= 3750 cm2

Jadi, luas permukaan kubus adalah 3750 cm2

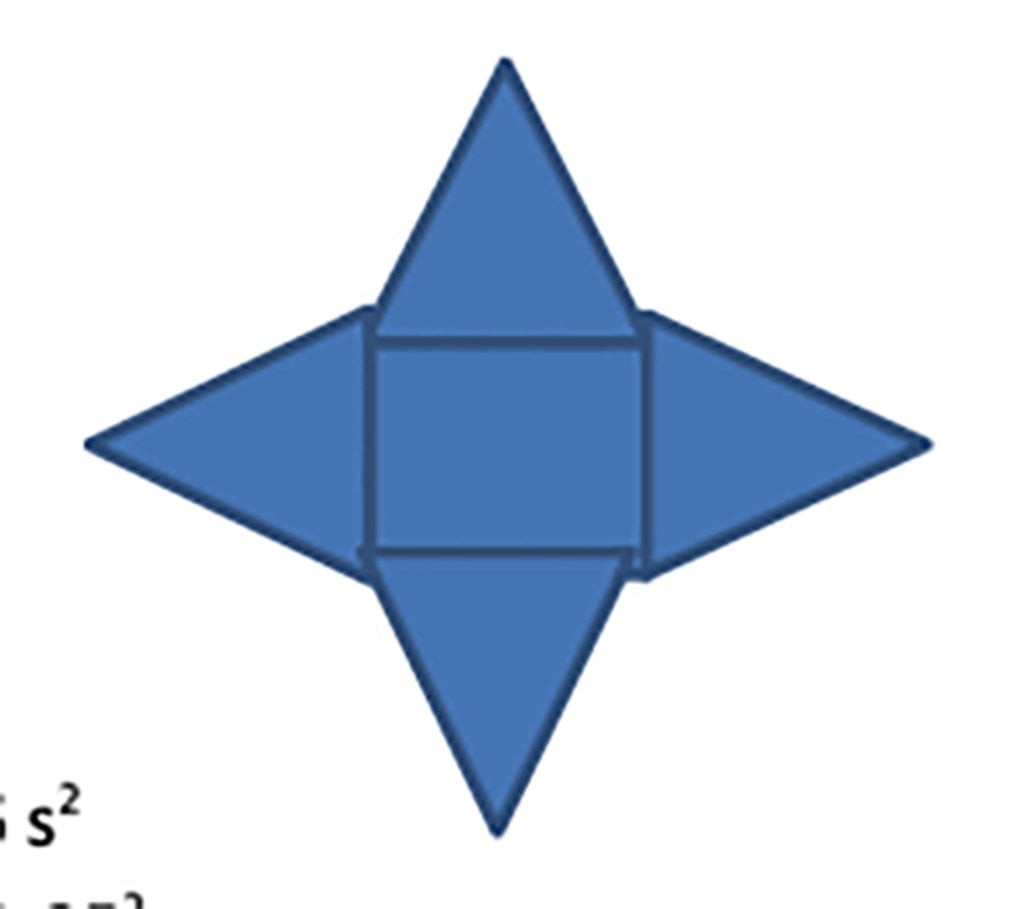
5. Gambarlah jaring-jaring limas yang alasnya berbentuk persegi!

Jawaban: