Soal OSN Matematika SD 2024 Tingkat Kecamatan & Jawabannya

tirto.id - OSN Matematika SD 2024 tingkat nasional digelar pada 5-11 Agustus 2024. Para peserta sebelumnya harus melewati tahapan sejak tingkat sekolah, kabupaten/kota, dan provinsi.

Matematika termasuk salah satu cabang lomba Olimpiade Sains Nasional Sekolah Dasar (OSN-SD) 2024. Cabang lainnya yaitu Ilmu Pengetahuan Alam (IPA).

OSN diselenggarakan secara bertahap. Terdiri dari fase sekolah atau Olimpiade Sains Nasional tingkat Sekolah (OSN-S) dan kabupaten/kota atau Olimpiade Sains Nasional tingkat Kab/Kota (OSN-K).

Kemudian provinsi atau Olimpiade Sains Nasional tingkat Provinsi (OSN-P) hingga menuju tingkat nasional alias Olimpiade Sains Nasional (OSN).

Tema OSN 2024 adalah "Merdeka Berprestasi, Talenta Sains Menginspirasi". Para siswa SD/MI/Sederajat akan saling berlomba demi menjadi yang terbaik.

Setidaknya, pihak panitia sudah menyiapkan 5 medali emas, 10 medali perak, dan 15 keping perunggu. Selain itu ada penghargaan honorable mention bagi peringkat 31-60 setiap cabang lomba .

Berikut jadwal lengkap pelaksanaan OSN SD 2024:

• Sosialisasi: 16-19 Januari 2024
• Pendaftaran Peserta OSN-SD: 22 Jan-3 Maret 2024
• Ujicoba aplikasi dan simulasi OSN-K: 13-16 Maret 2024
• Pelaksanaan OSN-K: 20-21 Maret 2024
• Pengumuman peserta yang lolos ke OSN-P: 15 April 2024
• Ujicoba aplikasi dan simulasi OSN-P: 1-4 Mei 2024
• Pelaksanaan OSN-P: 20-21 Mei 2024
• Pengumuman peserta OSN Tingkat Nasional: 3 Juni 2024
• Pelaksanaan OSN Tingkat Nasional: 5-11 Agustus 2024

Silabus Kisi-Kisi Materi Matematika OSN SD 2024

Silabus matematika mencakup 5 poin, yakni bilangan, aritmatika, geometri, statistika data dan pengukuran, serta kombinatorik.

Berikut adalah kisi-kisi materi cabang lomba matematika OSN SD 2024:

Bilangan

Materi bilangan terdiri dari beberapa macam. Di antaranya ialah:

• Bilangan Cacah
• Bilangan Bulat
• Bilangan Rasional
• Bilangan Prima
• Kelipatan Persekutuan Terkecil (KPK)
• Persekutuan Terbesar (FPB)
• Pola Bilangan

Aritmatika

Pada aritmatika, nantinya akan mempelajari materi berkaitan dengan:

• Operasi bilangan
• Persamaan linear satu variabel
• Persamaan linear dua variabel
• Sistem pertidaksamaan linear

Geometri

Geometri merupakan bahasan berikutnya. Beberapa materi yang dipelajari seperti berikut ini:

• Bidang datar, terdiri dari sifat-sifat bangun datar, segiempat, segitiga, lingkaran, luas, keliling, sudut, simetri lipat dan simetri putar.
• Geometri Ruang, mencakup volume, luas permukaan, dan jaring-jaring.

Statistika data dan pengukuran

Materi statistika data dan pengukuran meliputi sejumlah hal. Di antaranya ialah:

• Satuan waktu
• Hubungan antar satuan baku panjang, berat dan waktu
• Penyajian dan penjelasan diagram batang
• Pengumpulan dan penjelasan diagram batang
• Perbandingan dua besaran berbeda: kecepatan (jarak waktu), debit (volume-waktu)
• Pengumpulan dan analisis data
• Daftar, tabel, piktogram, diagram batang, diagram garis
• Modus, median, dan mean data tunggal

Kombinatorik

Sementara materi kombinatorik dibagi menjadi 2 macam, yakni:

• Penggunaan kombinasi dengan teknik counting problem
• Pengenalan pola dengan menggunakan kombinasi

Kumpulan Soal OSN Matematika SD 2024 Tingkat Kecamatan dan Jawabannya

Berikut adalah sejumlah contoh kumpulan soal OSN Matematika SD 2024 tingkat kecamatan lengkap beserta jawabannya:

1. Enam puluh persen peserta didik di suatu sekolah adalah laki-laki. Sebanyak 20% laki-laki dan 20% perempuan tidak memakai seragam batik. Jika diketahui ada 310 peserta didik memakai seragam batik, maka seluruh peserta didik yang ada di sekolah adalah....

Jawaban: 400 peserta

Pembahasan:

60%T laki laki jadi siswa perempuan ada 100-60 = 40%T

20% memakai seragam, yang tidak memakai seragam berarti 80%

80%x60% T + 80%x 40% T = 310

48/100 T + 32/100 T = 310

80/100 T=310

T= 310 x 100/80 (tidak bulat). Jika total peserta 320 maka:

T=320x100/80= 400 peserta.

2. Perhatikan kubus-kubus di bawah ini. Tentukan pasangan huruf-huruf yang berseberangan.

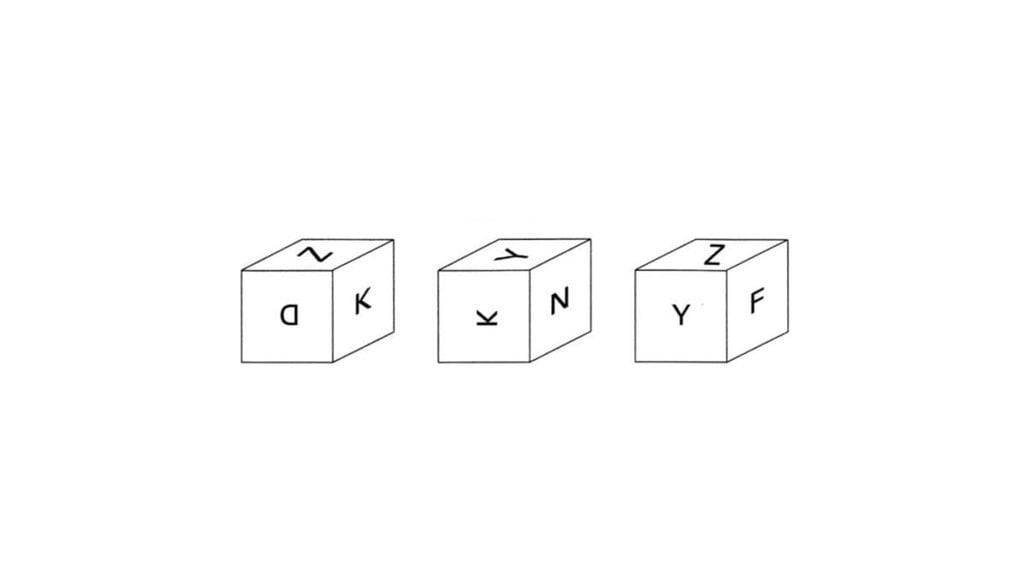
Jawaban:

Pembahasan: Y-D, K-F, N-Z

Pembahasan:

Berdasarkan kubus ke-2 dan ke-3, Y tidak berhadapan dengan K, N, Z, dan F.

Berdasarkan kubus ke-1 dan ke-2, K tidak berhadapan dengan D, Z, Y, dan N.

Sehingga diperoleh:

Y bersebrangan dengan D

K bersebrangan dengan F

N bersebrangan dengan Z

3. Dodi, Endang, Fahim dan Gafiz berlomba melempar batu. Hasil perlombaan diperoleh: 5% lemparan Endang lebih jauh dari lemparan Dodi, 8% lemparan Fahim lebih dekat dari lemparan Dodi, dan 10% lemparan Gafiz lebih jauh dari lemparan Dodi.

Jika rata-rata jarak lemparan mereka 305,25 dm, maka jarak lemparan Gafiz adalah …

Jawaban: 330 dm

Pembahasan:

Misal Dodi = 100x

Endang = 105x

Fahim = 92x dan Gafiz = 110x

Jarak total = 305,25 x 4

Dodi + Endang + Fahim + Gafiz = 1221

100x + 105x + 92x + 110x = 1221

407x = 1221

x = 1221/407 = 3

Jadi panjang lemparan Gafiz = 110 x = 110 x 3 = 330 dm

4. Umur Amir lebih tua tiga tahun dari umur Budi, Budi usianya lebih muda empat tahun dari Cipto, ketika usia Cipto 22 tahun, maka usia Amir adalah ....

Jawaban: 21 tahun

Pembahasan:

Misal:

A = Umur Amir

B = Umur Budi

C = Umur Cipto

A = B + 3

B = C - 4

C = 22

Mencari umur Budi:

B = C - 4

B = 22 - 4 = 18

A = B + 3

A = 18 + 3 = 21

Jadi, umur Amir adalah 21 tahun.

5. Sekelompok tentara mampu melakukan baris-berbaris sejauh 25 km pada saat tidak hujan dan 20 km pada saat hujan.

Jika mereka melakukan baris-berbaris itu sepanjang 480 km selama 20 hari, ada berapa jumlah hari hujan yang mereka lalui?

Jawaban: 4 hari hujan

Pembahasan:

Misal banyak hari tidak hujan adalah x

Banyak hari hujan adalah y

Diperoleh persamaan :

25 x + 20 y = 480 (i)

x + y = 20

x = 20-6 (ii)

Subtitusi persamaan (ii) ke dalam persamaan (i):

25 (20-y) + 20 y = 480

500 - 25 y + 20 y = 480

5 y = 20

y = 4

Jadi, ada 4 hari hujan

6. Pada pertandingan sepakbola suatu klub sepakbola akan memperoleh nilai 3 jika dia menang, memperoleh nilai 1 jika seri dan nilai 0 jika kalah.

Jika selama 25 kali pertandingan PS.OSN pernah seri dan memperoleh skor 48, maka klub PS.OSN paling sedikit memperoleh kekalahan … kali.

Jawaban: 1

Pembahasan:

kalah paling sedikit jika menang dan seri mendekati 25.

Menang = 12 x 3 = 36

Seri = 12 x 1 = 12

Jadi Kalah sebanyak = 25 – 12 – 12 = 1 kali

7. Ibu Vira memiliki 40 permen rasa mangga, 30 permen rasa melon, dan 50 permen rasa Jeruk. Apabila permen-permen tersebut akan dibagikan kepada sebanyak mungkin murid-muridnya dengan masing-masing anak mendapatkan bagian semua rasa yang sama banyak, maka banyak permen rasa Melon yang diberikan kepada setiap muridmuridnya adalah.....

Jawaban: 3 permen rasa melon setiap siswa.

Pembahasan:

FPB ( 30, 40 , 50 )

FPB = 10

Banyak permen rasa Melon adalah = 30/10 = 3 permen rasa melon setiap siswa.

8. Gambarlah sebuah garis lurus untuk membagi jam di samping menjadi dua bagian sehingga jumlah dari semua bilangan pada kedua bagian adalah sama.

Jawaban:

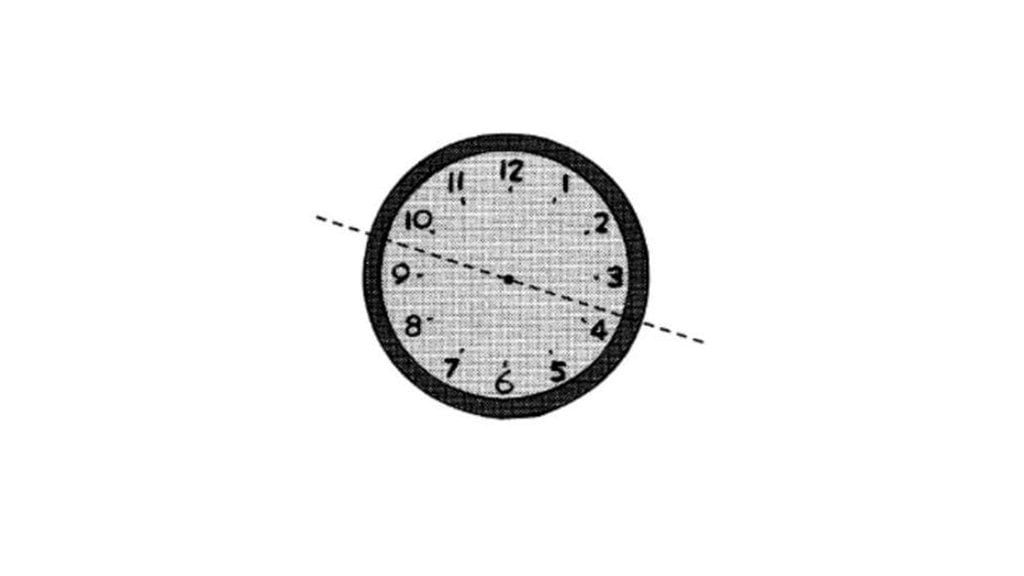
Pembahasan:

Jumlah bilangan pada jam = 1 + 2 + 3 + … + 11 + 12 = 78

Jumlah bilangan pada masing-masing bagian = 78 : 2 = 39

1+2+3+10+11+12=39

4+5+6+7+8+9=39

9. Selama mengikuti olimpiade matematika, Alya, Bilqis, Nurul dan Tiwi tinggal di kamar yang berbeda di sebuah hotel.

Alya harus turun empat lantai untuk mengunjungi Bilqis. Kamar Nurul satu lantai di bawah kamar Tiwi. Bilqis harus turun 10 lantai untuk ke tempat makan yang berada di lantai 1.

Tiwi harus naik enam lantai untuk mengunjungi Alya. Di lantai berapakah kamar Nurul?

Jawaban: Lantai 8

Pembahasan:

Diketahui :

A-4=B

N+1=T

B-10=1

T+6=A

Ditanyakan : N?

N + 1 = T

N = T - 1

N = (A-6) - 1

N = A - 7

N = (B + 4) - 7

N = B - 3

N = 11 - 3

N = 8

Jadi, kamar Nurul berada di lantai 8

10. Ibu Ani membeli 3 jenis pakaian yaitu : kaos, kemeja dan Celana. Ibu Ani membayar Rp1.400.000,00 untuk pembelian 3/4 lusin kaos, 1/2 lusin kemeja dan 1/4 kodi celana.

Jika harga satu celana dua kali lipat harga satu kaos dan total harga 1/2 lusin kemeja sama dengan total harga 3/4 lusin kaos, maka perbandingan harga satu kaos, satu kemeja dan satu celana adalah.....

Jawaban: 4 : 3 : 2

Pembahasan:

1 Celana = 2 x Kaos

Celana : Kaos = 2 : 1

1/2 lusin kemeja = harga 3/4 lusin kaos.

Jadi, 6 kemeja = 9 kaos

Kaos : Kemeja = 3 : 2

Celana : Kaos = 2 : 1

Kaos : Kemeja = 2 : 3

Celana : Kaos : Kemeja = 4 : 2 : 3

1 kaos : 1 kemeja : 1 celana = 4 : 3 : 2

11. Juliana mempunyai uang sebanyak Rp.73.000,00 yang terdiri dari pecahan lembaran uang 2000-an dan 1000-an.

Jika jumlah uang Juliana sebanyak 41 lembar, maka jumlah uang Juliana yang 2000-an saja adalah sebanyak Rp....

Jawaban: Rp64.000

Pembahasan:

(2.000 x 32) + (1.000 x 9) = 73.000

Jadi, jumlah uang Juliana yang 2000-an saja adalah sebanyak Rp64.000.

12. Dua bilangan jumlahnya 30 dan selisihnya 25. Hasil kali kedua bilangan itu adalah.....

Jawaban: 68,75

Pembahasan:

13. Jika masing-masing huruf A sampai huruf Z berpasangan dengan bilangan asli, Contoh : A = 1; B = 2 ; dan seterusnya, maka jumlah angka pada kalimat AKU SUKA MATEMATIKA adalah.....

Jawaban: 179

Pembahasan:

14. Dalam suatu perlombaan lari pada ajang Asian Games 10 orang pelari akan berlomba termasuk 2 orang pelari Indonesia Ari dan Eka. Rata-rata kecepatan 10 orang pelari adalah 11 km/jam.

Jika kecepatan Eka lebih lambat 3 km/jam dari kecepatan Ari dan rata-rata kecepatan keduanya adalah 12 km/jam, maka rata-rata kecepatan dari 9 orang pelari

selain Eka adalah ...

Jawaban: 11,056 km/jam

Pembahasan:

Misal 10 peserta adalah a, b, c, d, ..., j

15. Suatu lomba diadakan untuk memperingati hari Kemerdekaan Republik Indonesia. Perlombaan tersebut adalah mengumpulkan semua bendera yang ada di pos-pos yang telah ditentukan.

Setiap peserta diharuskan mengumpulkan satu bendera dari masingmasing pos. Jika setiap pos hanya bisa dilewati satu kali, maka banyak rute yang mungkin dilewati oleh peserta lomba adalah....

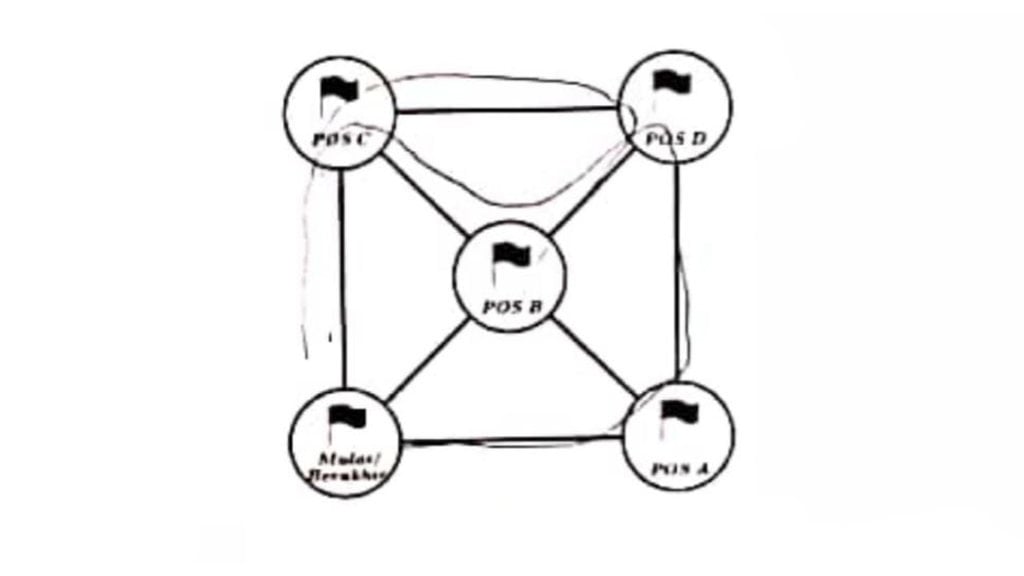
Jawaban: 8 rute

Pembahasan:

Rute yang bisa ditempuh

S – A – B – D – C

S – A – D – B – C

S – A – D – C – B (S – A) dan (S – C) sama ada 3 rute

S – B – C – D – A

S – B – A –D – C

Total rute = 3 + 3 + 2 = 8 rute

16. Perhatikan pola gambar di bawah ini

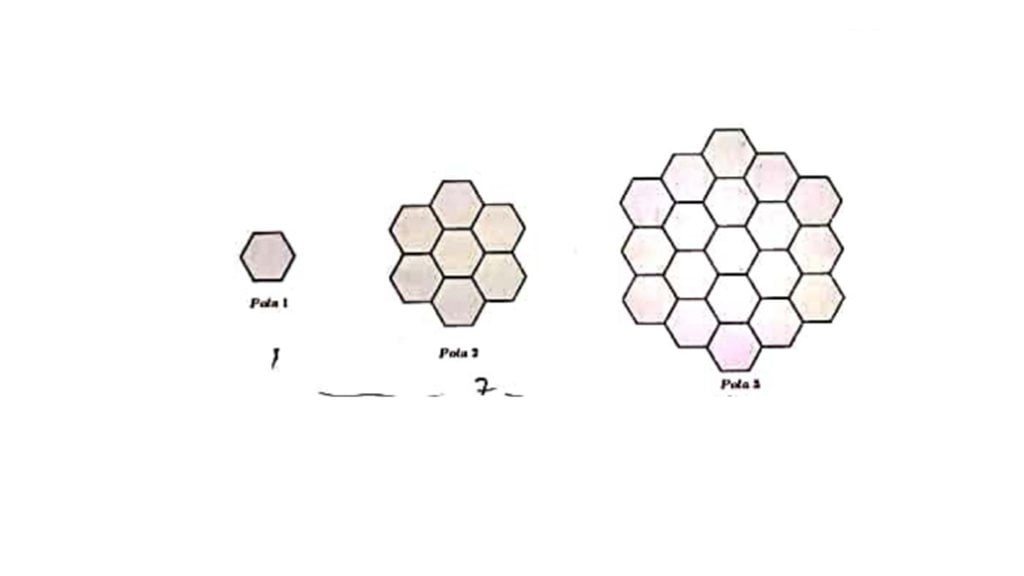
Banyaknya segi-6 pada pola 5 adalah.....

Jawaban: 61

Pembahasan:

Pola 1 =1

Pola 2 = 2 + 3 + 2

Pola 3 = 3 + 4 + 5 + 4 + 3

Pola 5 = 5 + 6 + 7 +8 +9 + 8 + 7 + 6 + 5 = 61