tirto.id - Rumus balok adalah macam-macam rumus untuk menghitung dimensi sebuah bangun ruang balok. Setidaknya ada empat jenis rumus dasar balok yang perlu diketahui.
Ketiga jenis rumus balok itu termasuk rumus volume balok, rumus luar permukaan balok, rumus keliling balok, dan rumus diagonal ruang balok.Rumus-rumus balok dapat dipelajari dengan mengerjakan contoh soalnya.
Namun, sebelum mengetahui apa rumus luas permukaan balok, rumus balok volume, maupun contoh soal balok, ada baiknya mengenal apa itu bangun ruang balok terlebih dahulu.
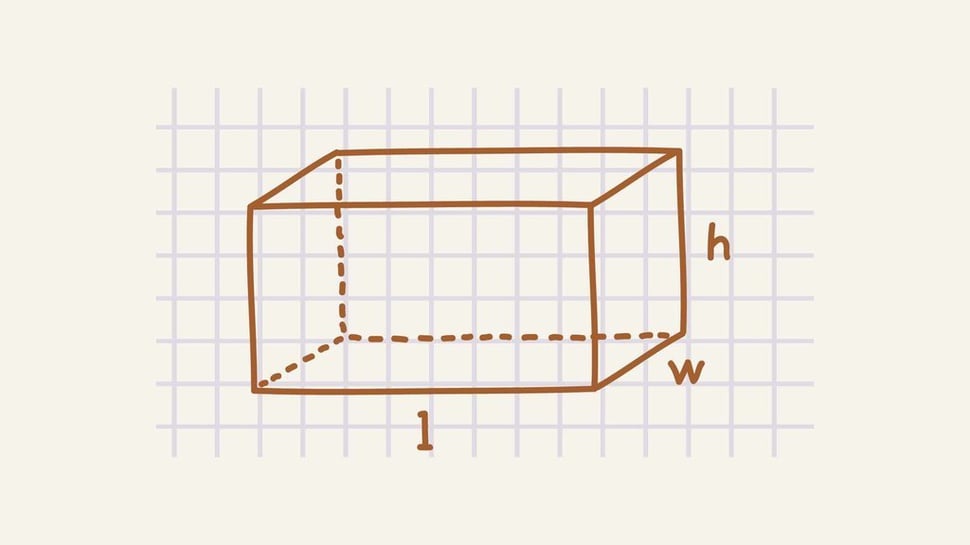
Dikutip dari Sumber Belajar Kemendikbud, balok adalah suatu bangun ruang yang dibatasi oleh enam persegi panjang. Setiap persegi panjang pada balok saing berimpit dan berhadapan satu sama lain.
Balok bisa dikenali dengan ciri-ciri berikut:
- Memiliki 6 sisi
- Sisi-sisinya yang saling berhadapan sejajar sama luas
- Memliki 12 rusuk
- Rusuk-rusuknya yang sejajar sama panjang
- Memiliki 8 titik sudut.
Rumus Volume Balok dan Luas Permukaan Balok
Rumus volume balok dan rumus luas permukaan balok merupakan dua rumus dasar untuk menghitung dimensi balok.
Rumus volume balok diterapkan untuk menghitung volume atau kapasitas ruang balok. Rumus balok volume dihitung dengan mengalikan panjang, lebar, serta tinggi balok.
Nantinya, hasil penghitungan volume balok dinyatakan dalam kubik seperti cm3, m3, dm3, dan sebagainya.
Lalu, untuk rumus luas permukaan balok dihitung dengan menjumlahkan hasil perkalian panjang, lebar, dan tinggi balok. Nantinya, hasil penjumlahan itu masih harus dikalikan dua sehingga ditemukan luas permukaan balok.
Selain rumus volume dan luas permukaan, ada dua rumus balok lainnya yang penting untuk diketahui. Kedua rumus balok itu adalah rumus keliling balok dan rumus luas diagonal balok.
Sesuai namanya, rumus keliling balok adalah rumus untuk menghitung keliling bangun ruang tersebut. Rumus ini bisa dihitung dengan menjumlahkan panjang, lebar, dan tinggi balok lalu hasilnya dikalikan 4.
Sementara itu, rumus diagonal ruang balok digunakan untuk menghitung luas ruang balok yang dibatasi oleh garis diagonal. Garis diagonal sendiri adalah garis yang menghubungkan antara sudut balok yang saling berhadapan.
Adapun rumus diagonal ruang balok dihitung dengan menjumlahkan panjang, lebar, dan tinggi balok dalam kuadrat. Selanjutnya hasil dari penjumlahan tersebut akan diakar untuk menemukan diagonalnya.
Dikutip dari laman Jateng Pintar milik Dinas Pendidikan dan Kebudayaan Provinsi Jawa Tengah, berikut daftar lengkap empat rumus balok:
1. Rumus Volume Balok
Volume = panjang x lebar x tinggi
2. Rumus Luas Permukaan Balok
Luas permukaan = 2 x ((panjang x lebar) + (panjang x tinggi) + (lebar x tinggi)) atau Luas = 2 x ((pxl) + (pxt) + (lxt))
3. Rumus Keliling Balok
Keliling = 4 x (p + l + t)
4. Rumus Diagonal Ruang Balok
Diagonal = √( p²+ l² + t² )
Contoh Soal-Soal Rumus Balok dan Penerapannya
Cara yang tepat untuk mempelajari rumus balok adalah dengan latihan contoh soal balok. Berikut contoh soal-soal untuk latihan penerapan rumus volume balok, rumus luas permukaan balok, rumus keliling balok, dan rumus diagonal balok:
Contoh soal 1
Sebuah kardus berbentuk balok memiliki panjang 24 cm, luas 8 cm, dan tinggi 48 cm. Hitunglah berapa volumenya!
Jawab:
Volume balok bisa dihitung dengan rumus berikut:
Volume = panjang x lebar x tinggi
Oleh karena itu, cara menjawab soal tersebut adalah dengan langkah-langkah berikut:
Volume = 24 x 8 x 48
Volume = 192 x 48
Volume = 9.216 cm3
Jawabannya, volume kardus berbentuk balok tersebut adalah 9.216 cm3.
Contoh soal 2
Diketahui sebuah benda berbentuk balok memiliki lebar 7 cm, panjang 6 cm, dan tinggi 8 cm. Berapakah volume balok tersebut?
Jawab:
Volume balok bisa dihitung dengan rumus berikut:
Volume = panjang x lebar x tinggi
Sama seperti soal di atas, berikut cara menjawab soal tersebut:
Volume = 6 x 7 x 8
Volume = 42 x 8
Volume = 336 cm3
Jawabannya, volume benda berbentuk balok tersebut adalah 336 cm3.
Contoh soal 3
Sebuah kotak kado berbentuk balok memiliki volume 630 cm3, dengan panjang 10 cm dan lebar 9 cm. Berapakah tinggi kotak kado tersebut?
Jawab:
Mencari tinggi balok yang sudah diketahui volumenya bisa menggunakan rumus volume balok berikut:
Volume = panjang x lebar x tinggi
Berikut langkah-langkah menjawabnya:
630 = 10 x 9 x t
630 = 90 x t
630/90 = t
7 = t
Jawabannya, tinggi kotak kado berbentuk balok tersebut adalah 7 cm.
Contoh soal 4
Sebuah balok memiliki ukuran panjang 8 cm, lebar 6 cm, dan tinggi 7 cm. Hitunglah berapa luas permukaan balok tersebut!
Jawab:
Luas permukaan balok bisa dihitung menggunakan rumus:
Luas = 2 x ((pxl) + (pxt) + (lxt))
Berikut cara menjawabnya:
Luas = 2 x ((8x6) + (8x7) + (6x7))
Luas = 2 x (48 + 56 + 48)
Luas = 2 x 146
Luas = 292 cm²
Jawabannya, luas permukaan balok tersebut adalah 292 cm².
Contoh soal 5
Diketahui sebuah kotak pensil berbentuk balok memiliki panjang 12 cm, lebar 5 cm, dan tinggi 3 cm. Berapakah luas permukaan kotak pensil tersebut?
Jawab:
Sama seperti soal sebelumnya, luas permukaan kotak pensil bisa dihitung menggunakan rumus:
Luas = 2 x ((pxl) + (pxt) + (lxt))
Berikut cara menjawabnya:
Luas = 2 x ((12x5) + (12x3) + (5x3))
Luas = 2 x (60 + 36 + 15)
Luas = 2 x 111
Luas = 222 cm²
Jawabannya, luas permukaan balok tersebut adalah 222 cm².
Contoh soal 6
Sebuah bangun balok memiliki luas permukaan 920 cm². Sementara itu, panjang balok adalah 10 cm dan tingginya 25 cm. Berapakah lebar balok tersebut?
Jawab:
Lebar balok yang sudah diketahui panjang, tinggi, dan luas permukaannya bisa dihitung menggunakan rumus luas permukaan sebagai berikut:
Luas = 2 x ((pxl) + (pxt) + (lxt))
Berikut langkah-langkah menghitungnya:
920 = 2 x ((10x l) + (10 x 25) + (l x 25)
920 = 2 x (10l + 250 + 25l)
920 = 2 x (250 + 35l)
920 = 500 + 70l
920 - 500 = 70l
420 = 70l
420/70 = l
6 = l
Jawabannya, lebar balok tersebut adalah 6 cm.
Contoh soal 7
Sebuah balok memiliki panjang 9 cm, lebar 5 cm, dan tinggi 13 cm. Berapakah keliling balok tersebut?
Jawab:
Keliling balok bisa dihitung menggunakan rumus keliling balok, yaitu:
Keliling = 4 x (p + l + t)
Berikut cara menerapkannya dalam soal:
Keliling = 4 x (9 + 5 + 13)
Keliling = 4 x 27
Keliling = 100 cm
Jawabannya, keliling balok tersebut adalah 100 cm.
Contoh soal 8
Diketahui sebuah kardus berbentuk balok mempunyai lebar 10 cm, tinggi 6 cm, dan panjang 8 cm. Hitunglah keliling kardus tersebut!
Jawab:
Sama seperti soal sebelumnya, keliling kardus tersebut bisa dihitung menggunakan rumus keliling balok sebagai berikut:
Keliling = 4 x (p + l + t)
Berikut langkah-langkahnya:
Keliling = 4 x (8 + 10 + 6)
Keliling = 4 x 24
Keliling = 96 cm
Jawabannya, keliling balok tersebut adalah 96 cm.
Contoh soal 9
Sebuah balok memiliki keliling 56 cm, dengan panjang 8 cm, dan lebar 3 cm. Berapakah tinggi balok tersebut?
Jawab:
Tinggi sebuah balok yang sudah diketahui keliling, panjang, dan lebarnya bisa dihitung menggunakan rumus keliling, yaitu:
Keliling = 4 x (p + l + t)
Berikut langkah-langkah penerapannya:
56 = 4 x (8 + 3 + t)
56 = 4 x (11 + t)
56 = 44 + 4t
56 - 44 = 4t
12 = 4t
12/4 = t
3 = t
Jawabannya, tinggi balok tersebut adalah 3 cm.
Contoh soal 10
Diketahui sebuah balok memiliki panjang 6 cm, lebar 8 cm, dan tinggi 15 cm. Tentukan panjang diagonal balok tersebut!
Jawab:
Panjang diagonal balok bisa ditemukan lewat rumus berikut:
Diagonal = √( p²+ l² + t² )
Berikut langkah-langkah penerapannya:
Diagonal = √( 6²+ 8² + 15² )
Diagonal = √(36 + 64 + 225)
Diagonal = √325
Diagonal = 5√13 cm
Jawabannya, panjang diagonal balok tersebut adalah 5√13.
Contoh soal 11
Sebuah kotak berbentuk balok memiliki panjang 15 cm, lebar 10 cm, dan tinggi 4 cm. Berapakah diagonal balok tersebut?
Jawab:
Sama seperti soal di atas diagonal balok bisa ditemukan lewat rumus berikut:
Diagonal = √( p²+ l² + t² )
Berikut langkah-langkah penerapannya:
Diagonal = √( 15²+ 10² + 4² )
Diagonal = √(225 + 100 + 16)
Diagonal = √341
Diagonal = 18√17 cm
Jawabannya, panjang diagonal balok tersebut adalah 18√17.
Contoh soal 12
Sebuah balok memiliki panjang 20 cm, lebar 6 cm, dan tinggi 8 cm. Tentukan berapa panjang diagonal balok tersebut!
Jawab:
Diagonal balok bisa ditemukan lewat rumus berikut:
Diagonal = √( p²+ l² + t² )
Berikut langkah-langkah penerapannya:
Diagonal = √( 20²+ 6² + 8² )
Diagonal = √(400 + 36 + 64)
Diagonal = √500
Diagonal = 10√5 cm
Jawabannya, panjang diagonal balok tersebut adalah 10√5 cm.
Editor: Dhita Koesno