Rumus Luas dan Keliling Layang-layang Beserta Contoh Soalnya

tirto.id - Rumus layang-layang dapat dipakai untuk menghitung ukuran luas dan keliling dalam beberapa contoh soal. Materi bangun datar ini diajarkan sejak jenjang sekolah dasar.

Selain layang-layang, siswa juga mempelajari rumus bangun datar lain, mulai dari persegi, persegi panjang, jajar genjang, segitiga, hingga lingkaran.

Masing-masing bangun datar memiliki rumus luas dan keliling yang berbeda, sesuai sifatnya.

Untuk itu, sebelum mempelajari rumus luas dan keliling layang-layang, serta mencoba mengerjakan contoh soal, alangkah lebih baiknya jika memahami sifat layang-layang terlebih dahulu.

Apa Saja Sifat Layang-layang?

Layang-layang adalah turunan dari segi empat, dibentuk oleh dua pasang sisi yang masing-masing pasangannya sama panjang serta saling membentuk sudut.

Sesuai definisi di atas, layang-layang tergolong segi empat, sama dengan persegi dan persegi panjang. Namun, bentuk antara kedua bangun datar tersebut berbeda.

Berikut ini ciri-ciri dan sifat layang-layang:

• Layang-layang memiliki 2 diagonal yang saling berpotongan pada sudut siku-siku.
• Layang-layang simetris terhadap diagonal utamanya.
• Sudut-sudut yang berlawanan dengan diagonal utama adalah sama besar.
• Layang-layang dapat dilihat sebagai sepasang segitiga yang tergolong sebagai cerminan, alias bentuk dan ukurannya sama persis.
• Diagonal yang lebih pendek membagi layang-layang menjadi dua buah segitiga sama kaki.

Untuk memahami lebih jelas sifat layang-layang dapat melihat gambar sebagai berikut:

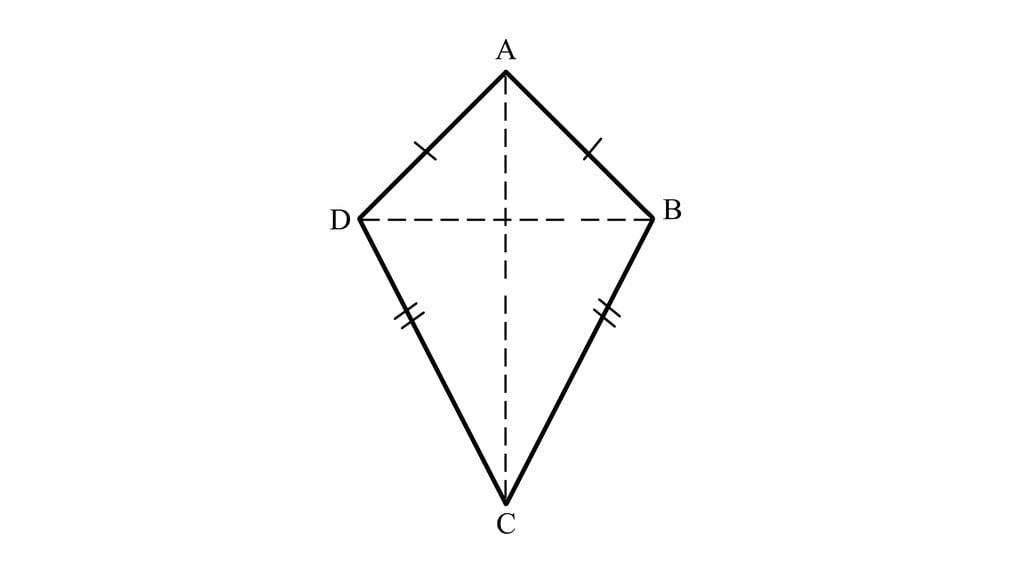
Dari gambar layang-layang di atas, diperoleh keterangan beberapa sifat layang-layang sebagai berikut:

• Layang-layang memiliki 4 sisi meliputi AB, BC, CD, dan DA.
• Sisi yang berdekatan di layang-layang memiliki panjang sama meliputi AB = DA dan BC = CD.
• Diagonal layang-layang saling berpotongan dan tegak lurus yakni garis AC ⊥ BD.
• Layang-layang memiliki 4 sudut meliputi ABC, BCD, CDA, dan DAB.
• Layang-layang memiliki sepasang sudut yang berhadapan sama besar meliputi ABC = CDA.

Untuk lebih memahami sifat layang-layang, Anda bisa mencermati beberapa contoh benda yang berbentuk layang-layang. Berikut ini contoh benda apa saja yang berbentuk layang-layang:

• Bentuk tas
• Layang-layang
• Biji mata buah nanas
• Pagar
• Penggaris siku-siku yang didekatkan
• Relief Candi Borobudur
• Variasi bentuk jendela
• Variasi model anting
• Ventilasi rumah

Apa Rumus Luas dan Keliling Layang-layang?

Rumus luas dan keliling layang-layang dapat dihafal dengan mudah selagi dapat memahami konsepnya dengan baik. Sebelumnya Anda dapat mencermati gambar berikut ini untuk mulai mencermati cara kerja rumus luas dan keliling layang-layang:

1. Rumus Luas Layang-Layang

Luas layang layang diperoleh dengan menggunakan rumus ½ dikalikan kedua diagonal. Layang-layang di atas memiliki dua diagonal, yakni AC dan DB. Rumus luas layang-layang dapat dituliskan sebagai berikut:

L = ½ ⋅ Diagonal₁ ⋅ Diagonal₂

Lantas, dari mana asal usul rumus luas dan keliling layang-layang di atas? Bagaimana pembuktian rumus keliling layang itu?

1. Diagonal adalah garis yang membagi layang-layang menjadi dua bagian.
2. Diagonal₁ adalah AC, yang membuat layang-layang terbelah menjadi dua, dan membentuk dua segitiga, yakni segitiga ABC dan ACD.
3. Diagonal₂ adalah BD. Konsepnya sama. Hanya bentuk segitiganya yang berbeda. Kali ini, ada dua segitiga sama kaki, yakni ABD dan BCD.
4. Untuk membuktikan rumus luas, kita bisa menggunakan salah satu rumusan, antara poin (2) atau poin (3).
5. Anggap saja kita menggunakan poin (2), sebab dasarnya sama saja.
6. Berdasarkan poin (2), kita memiliki layang-layang, yang terdiri atas dua segitiga: ABC dan ACD. Untuk mengetahui luasnya, kita harus menghitung luas dua segitiga tersebut, kemudian menjumlahkannya.

Untuk membuat pembuktian rumus luas layang-layang, diperoleh perhitungan sebagai berikut:

L ABCD = L ABC + L ACD

= ½ ⋅ alas ⋅ tinggi + ½ ⋅ alas ⋅ tinggi

= ½ ⋅ AC ⋅ OB + ½ ⋅ AC ⋅ OD

= ½ ⋅ AC ⋅ (OB + OD)

= ½ ⋅ AC ⋅ BD

Pada layang-layang di atas, AC dan BD merupakan diagonal. Jadi, terbukti bahwa rumus luas layang-layang adalah setengah dikali diagonal₁ dikali diagonal₂.

Sebagai catatan, rumus luas (L) segitiga = ½ ⋅ alas ⋅ tinggi. Sementara itu, 'O' adalah simbol untuk menggambarkan titik tengah yang terbentuk dari potongan diagonal.

2. Rumus Keliling Layang-Layang

Rumus keliling layang-layang diperoleh dari perhitungan seluruh panjang sisi layang-layang, yang mencakup sisi AB, BC, CD, dan DA.

Rumus keliling layang-layang dapat dituliskan dalam bentuk matematika sebagai berikut:

K = AB + BC + CD + DA

atau,

K = sisi₁ + sisi₂ + sisi₃ + sisi₄

Kalau dirasa terlalu panjang, pembuktian rumus keliling layang-layang di atas dapat diringkas menjadi rumus yang lebih simpel.

Seperti dijelaskan dalam subbab sifat layang-layang sebelumnya, layang-layang memiliki dua sisi yang panjangnya sama. Panjang AB sama dengan AD, sementara BC sama dengan DC.

Maka, kita bisa meringkas perhitungannya dengan cukup menjumlahkan AB dan BC. Kemudian , hasil penjumlahan itu dikalikan dua.

Dalam rumus matematika, rumus keliling layang-layang bisa ditulis ringkas sebagai berikut:

K = 2 ⋅ (BC + CD)

atau

K = 2 ⋅ (sisi₁ + sisi₂)

Sebagai catatan, penamaan sisi₁ dan sisi₂ digunakan untuk memisahkan sisi yang panjangnya berbeda.

Contoh Soal Luas Layang-layang dan Keliling

Rumus luas dan keliling layang-layang lebih mudah dipahami jika Anda mencoba mengerjakan contoh soal. Berikut ini contoh soal luas layang-layang dan kelilingnya, disertai cara mengerjakan dan jawabannya.

Contoh soal 1

Apabila sebuah layang-layang memiliki panjang diagonal 40 cm dan 35 cm, berapa luas layang-layang tersebut?

Diketahui:

• Panjang diagonal 1 (P d₁) = 40 cm
• Panjang diagonal 2 (P d₂) = 35 cm

Jawaban:

• L = ½ ⋅ Diagonal₁ ⋅ Diagonal2

  L = ½ x 40 cm x 35 cm

  L = 700 cm²

Contoh soal 2

Sebuah layang-layang memiliki panjang sisi 4 cm, 4 cm, 6 cm, dan 6 cm. Berapa keliling layang-layang tersebut?

Diketahui:

• Sisi layang-layang = 4 cm, 4 cm, 6 cm, dan 6 cm

Jawaban:

• K = sisi₁ + sisi₂ + sisi₃ + sisi₄
• K = 4 cm + 4 cm + 6 cm + 6 cm
• K = 20 cm

atau,

• K = 2 ⋅ (4+6)

  K = 2 ⋅ 10

  K = 20 cm

Contoh soal 3

Sebuah layang-layang memiliki keliling 50 cm. Kemudian salah satu sisinya mempunyai panjang 9 cm. Berapa sisi layang-layang yang lain?

Diketahui:

• Layang-layang memiliki 4 sisi. Dua sisi yang berhadapan panjangnya sama.
• Salah satu sisi 9 cm, maka sisi 1 lainnya juga 9 cm.
• Anggap saja sisi₁ = 9 cm, dan sisi₄ = 9 cm. Jadi, yang belum diketahui adalah sisi₂ dan sisi₃

Jawaban:

• K = sisi₁ + sisi₂ + sisi₃ + sisi₄

  50 = 9 + sisi₂ + sisi₃ + 9

  50 = 18 + sisi₂ + sisi₃

  50 - 18 = sisi₂ + sisi₃

  32 = sisi₂ + sisi₃

  32 = 16 + 16

Karena panjang sisi₂ dan sisi₃ adalah sama, dapat disimpulkan bahwa 32 cm merupakan penjumlahan dari dua sisi tersebut. Jadi, sisi₂ panjangnya 16 cm, begitu juga sisi₃

Jadi, panjang sisi yang lain dari layang-layang di atas adalah 16 cm.

Contoh soal 4

Ada sebuah layang-layang ABCD, dengan keliling 102 cm. Panjang BC sama dengan dua kali lipat sisi AB. Berapa panjang keempat sisinya?

Diketahui:

• K = 102
• AB = DA
• BC = CD
• BC = (2 ⋅ AB)

Jawaban:

• K = AB + BC + CD + DA

  102 = AB + (2 ⋅ AB) + (2 ⋅ AB) + AB

  102 = 6 ⋅ AB

  AB = 102/6 cm

Jadi, panjang sisi AB adalah 17 cm.

Karena AB = 17, DA juga 17 cm. Dengan begitu, kita bisa mencari panjang sisi yang lain.

• K = AB + BC + CD + DA
• 102 = 17 + BC + CD + 17
• 102 = 34 + BC + CD
• 102 - 34 = BC + CD
• 68 = BC + CD
• 68 = 34 + 34

Jadi, dapat disimpulkan bahwa panjang seluruh sisi layang-layang ABCD, secara berurutan, meliputi: 17 cm, 17 cm, 34 cm, dan 34 cm.