tirto.id - Rangkuman materi Polinomial kelas 11 Kurikulum Merdeka ini dapat dijadikan bahan referensi bagi tenaga pendidik yang akan mempersiapkan bahan pembelajaran sekaligus perangkat ajar untuk memasuki tahun ajaran baru yang sudah dimulai.
Materi polinomial dalam Kurikulum Merdeka ini merupakan salah satu bentuk materi Matematika tingkat lanjut. Polinomial ini sendiri, sebagaimana dirujuk dari buku Matematika Tingkat Lanjut terbitan Kemdikbud, berarti bentuk aljabar yang berupa monomial atau penjumlahan dari dua atau lebih monomial.
Dengan mempelajari Polinomial dalam Kurikulum Merdeka, para siswa kelas 11 diharapkan dapat berpikir tingkat tinggi, kritis, mampu memecahkan masalah yang rumit, lebih kreatif dan inovatif, komunikatif, kolaboratif, serta melek teknologi, khususnya teknologi digital di era revolusi industri 4.0 seperti saat ini.
Lantas, materi apa saja yang dipelajari dalam Polinomial kelas 11 Kurikulum Merdeka ini?
Materi Polinomial Kelas 11 Kurikulum Merdeka
Dalam materi Polinomial kelas 11 Kurikulum Merdeka, siswa akan mendapatkan sejumlah materi yang dijabarkan dalam sejumlah subbab.
Subbab-subbab itu berisi materi-materi seperti di bawah ini:
A. Polinomial dan Fungsi Polinomial
Pada subbab ini siswa kelas 11 akan mempelajari polinomial dan fungsi polinomial. Siswa juga akan diajak untuk menganalisis suatu polinomial dengan mengidentifikasi derajat dari polinomial tersebut.1. Pengertian Polinomial
Sebelum melihat definisi formal dari polinomial, kerjakan aktivitas eksplorasi berikut untuk mengenal penyusun dari polinomial, yaitu monomial.
Monomial adalah suatu bilangan, suatu variabel berpangkat bilangan cacah, atau perkalian antara bilangan dan satu atau lebih variabel-variabel berpangkat bilangan cacah. Konstanta merupakan monomial yang tidak memuat variabel, misalnya –8 dan 25. Faktor numerik dari suatu monomial disebut dengan koefisien.
Monomial merupakan salah satu jenis polinomial. Seperti pada bilangan real, jika kita menjumlahkan dua bilangan real akan menghasilkan bilangan real. Penjumlahan dari dua atau lebih monomial juga merupakan polinomial.
Untuk lebih jelasnya, perhatikan definisi polinomial berikut.
Definisi Polinomial: Polinomial adalah bentuk aljabar yang berupa monomial atau penjumlahan dari dua atau lebih monomial.
Untuk lebih memahami polinomial, perhatikan Contoh 2.1 berikut ini:

2. Derajat Suatu Polinomial
Salah satu karakteristik dari polinomial adalah derajatnya.Jika telah mengetahui bagaimana menentukan derajat dari suatu monomial, siswa dapat dengan mudah dapat mengidentifikasi derajat dari suatu polinomial.
Derajat Monomial: Jika a adalah koefisien yang tak nol, derajat monomial ax n adalah n. Derajat suatu monomial yang terdiri dari beberapa variabel adalah jumlah dari eksponen semua variabel tersebut.
Setiap suku dari polinomial merupakan monomial. Oleh karena itu, penentuan derajat suatu polinomial tergantung dari monomial-binomial yang menjadi suku dari polinomial tersebut.
Definisi Derajat Polinomial adalah derajat suatu polinomial adalah derajat dari sukunya yang berderajat tertinggi.
Untuk lebih memahami derajat polinomial, cermati contoh 2.2 berikut ini:

3. Fungsi Polinomial
Bentuk polinomial dapat digunakan untuk mendefinisikan suatu fungsi. Serupa dengan bentuk polinomial, fungsi polinomial juga memiliki derajat. Derajat dari fungsi polinomial yang disebutkan dalam definisi tersebut adalah n. Suku dari fungsi polinomial yang memiliki derajat tertinggi disebut dengan suku utama. Koefisien dari suku utama tersebut dinamakan koefisien utama.
Karakteristik dari suatu fungsi dapat dilihat dari grafiknya. Demikian juga dengan fungsi polinomial. Perhatikan Contoh 2.3 berikut untuk mengetahui bagaimana menggambar grafik fungsi polinomial.
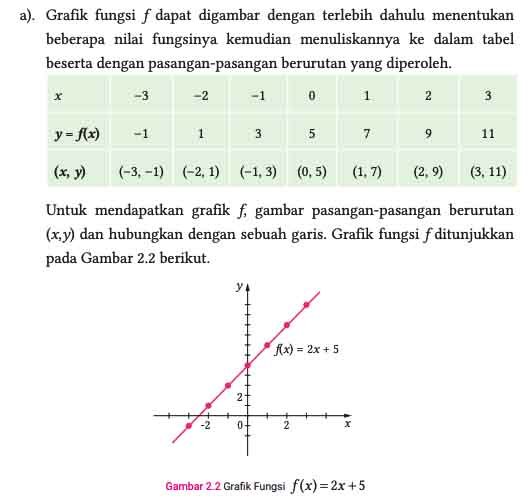
Gambarlah grafik dari fungsi f(x)=2x+5
B. Penjumlahan, Pengurangan, dan Perkalian Polinomial
1. Penjumlahan dan Pengurangan Polinomial
Polinomial memiliki hubungan yang dekat dengan bilangan. Untuk melakukan penjumlahan dan pengurangan polinomial, para siswa harus menjumlahkan dan mengurangkan suku-sukunya yang sejenis.
Suku-suku sejenis adalah suku-suku yang memiliki variabel yang sama dan variabelnya tersebut juga memiliki eksponen yang sama.
Untuk mendapatkan gambaran yang lebih jelas mengenai penjumlahan dan pengurangan polinomial, perhatikan contoh berikut ini:

2. Perkalian Polinomial
Perkalian polinomial dapat dibangun melalui perkalian bilangan.
Perhatikan contoh berikut ini untuk mengetahui bagaimana perkalian polinomial dilakukan.

C. Pembagian Polinomial
Pembagian pada polinomial, serupa dengan pembagian bilangan. Pembagian pada polinomial tersebut dinyatakan dalam algoritma pembagian.
Berikut ini adalah contoh dari algoritma pembagian polinomial.

Selanjutnya, perhatikan contoh berikut untuk mengetahui bagaimanakah pengoperasan pembagian polinomial bersusun:

Teorema Sisa adalah sisa-sisa pembagian suku banyak tanpa mengetahui suku banyak atau hasil baginya. Pengoperasiannya adalah berikut ini:
Jika polinomial P(x) dibagi dengan x-c, maka sisanya sama dengan P(c).
Teorema sisa tersebut dapat dibuktikan dengan menggunakan algoritma pembagian dan fakta bahwa derajat dari sisa pembagian selalu kurang dari polinomial pembagi. Untuk memahami teorema sisa ini perhatikan contoh berikut ini:

D. Faktor dan Pembuat Nol Polinomial
Teorema Faktor
Jika suatu polinomial P(x) dibagi dengan x – c, salah satu kemungkinannya adalah bahwa pembagian tersebut menghasilkan sisa nol. Berdasarkan Teorema Sisa, kita dapat menyimpulkan bahwa P(c) = 0. Dengan kata lain, c adalah pembuat nol P.
Untuk mengetahui penggunaan teorema faktor, perhatikan contoh berikut ini:

Selanjutnya, untuk mengetahui bagaimana menggunakan teorema faktor dan pembuat nol rasional, coba perhatikan contoh berikut ini:

E. Identitas Polinomial
Identitas polinomial adalah persamaan polinomial yang selalu benar untuk kemungkinan setiap variabel. Perhatikan contoh berikut untuk mengetahui apa saja identitas polinomial itu.

Untuk membuktikan bahwa suatu persamaan merupakan identitas, kita perlu menunjukkan bahwa bentuk yang di ruas kiri persamaan tersebut sama dengan yang di ruas kanan untuk setiap kemungkinan nilai variabelnya.
Sebaliknya, jika kita ingin menunjukkan bahwa suatu persamaan bukan merupakan identitas, kita cukup memberikan satu contoh nilai variabel yang membuat bentuk di ruas kiri persamaan tersebut tidak sama dengan bentuk yang di ruas kanan.
Perhatikan contoh berikut ini untuk memahami dan membuktikan identitas polinomial:

Penulis: Lucia Dianawuri
Editor: Yulaika Ramadhani












