Apa Saja Unsur-Unsur Prisma? Simak Penjelasan Lengkapnya

tirto.id - Unsur unsur prisma perlu dipahami ketika mempelajari ilmu matematika. Dengan memahami unsur dan sifat prisma secara keseluruhan, kita bisa menguasai konsep dasar geometri serta menghitung luas, volume, dan karakteristik bangun ruang lainnya.

Prisma adalah bangun ruang yang dibatasi oleh alas dan tutup identik. Alas dan tutup ini berupa dua bidang sejajar yang memiliki bentuk serta ukuran yang sama. Kedua bidang yang kongruen ini dihubungkan dengan sisi-sisi berupa bidang datar yang umumnya berbentuk segi empat.

Prisma terdiri dari bermacam-macam jenis dan diberi nama sesuai dengan bentuk poligon alas/tutupnya, misalnya prisma segitiga, prisma segi empat, dan seterusnya.

Bangun ruang prisma dapat ditemui dalam kehidupan sehari-hari. Misalnya, kotak pensil yang berbentuk prisma segi empat, lalu ada tenda kemah, atap rumah, atau sandwich yang berbentuk prisma segitiga, dan masih banyak lagi.

Prisma sendiri memiliki unsur-unsur yang berkaitan langsung dengan karakteristik bentuknya. Unsur unsur prisma sebagai bangun ruang antara lain:

• Sisi: bidang atau bangun datar yang membentuk bangun ruang
• Rusuk: garis pertemuan antara dua sisi pada bangun ruang
• Titik sudut: titik pertemuan dua rusuk atau lebih yang biasanya terletak di ujung atau pojok bangun ruang.
• Diagonal sisi: garis yang menghubungkan dua titik sudut yang berlawanan di setiap sisi.
• Diagonal ruang: garis yang menghubungkan dua titik sudut yang saling berhadapan atau berseberangan dan tidak berada pada satu bidang yang sama.
• Bidang diagonal: bidang yang dibatasi oleh dua rusuk dan dua diagonal sisi.

Unsur-Unsur Prisma

Dalam matematika, unsur unsur prisma terdiri dari enam hal yang berkaitan dengan jumlah sisi, rusuk, sudut, hingga bidang diagonal. Selain dihitung secara manual, setiap unsur ini juga dapat diketahui melalui rumus tertentu sebagai berikut:

• Rumus jumlah sisi/bidang pada prisma segi-n: n+2
• Rumus jumlah rusuk pada prisma segi-n: 3n
• Rumus jumlah titik sudut pada prisma segi-n: 2n
• Rumus jumlah diagonal bidang pada prisma segi-n: n(n-1)
• Rumus jumlah diagonal ruang pada prisma segi-n: n(n-3)
• Rumus jumlah bidang diagonal pada prisma segi-n: n/2 x (n-1)

Dengan adanya rumus ini, kita bisa mengetahui unsur unsur prisma dengan lebih mudah. Untuk lebih jelasnya, berikut unsur-unsur prisma berdasarkan jenisnya:

Prisma Segitiga

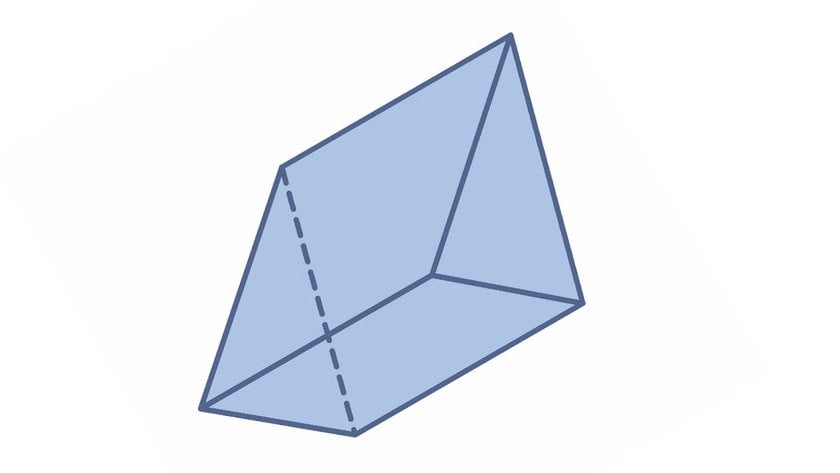
Prisma segitiga adalah sebuah bangun ruang tiga dimensi yang memiliki alas dan tutup berbentuk segitiga yang kongruen (sama besar dan bentuk) dan sejajar satu sama lain. Sementara sisi-sisi lainnya menghubungkan bagian alas dan tutup serta memiliki bentuk persegi panjang. Adapun unsur-unsur prisma segitiga adalah sebagai berikut:

1. Sisi/bidang

n+2 = 3 + 2 = 5

Jadi, prisma segitiga memiliki 5 buah sisi atau bidang.

2. Rusuk

3n = 3 x 3 = 9

Jadi, prisma segitiga memiliki 9 buah rusuk.

3. Titik sudut

2n = 2 x 3 = 6

Jadi, prisma segitiga memiliki 6 buah titik sudut.

4. Diagonal sisi

n(n-1) = 3(3-1) = 6

Jadi, prisma segitiga memiliki 6 buah diagonal sisi.

5. Diagonal ruang

n(n-3) = 3(3-3) = 0

Jadi, prisma segitiga tidak memiliki diagonal ruang.

6. Bidang diagonal

n/2 x (n-1) = 3/2 x (3-1) = 3

Jadi, prisma segitiga memiliki 3 bidang diagonal

Prisma Segi Empat

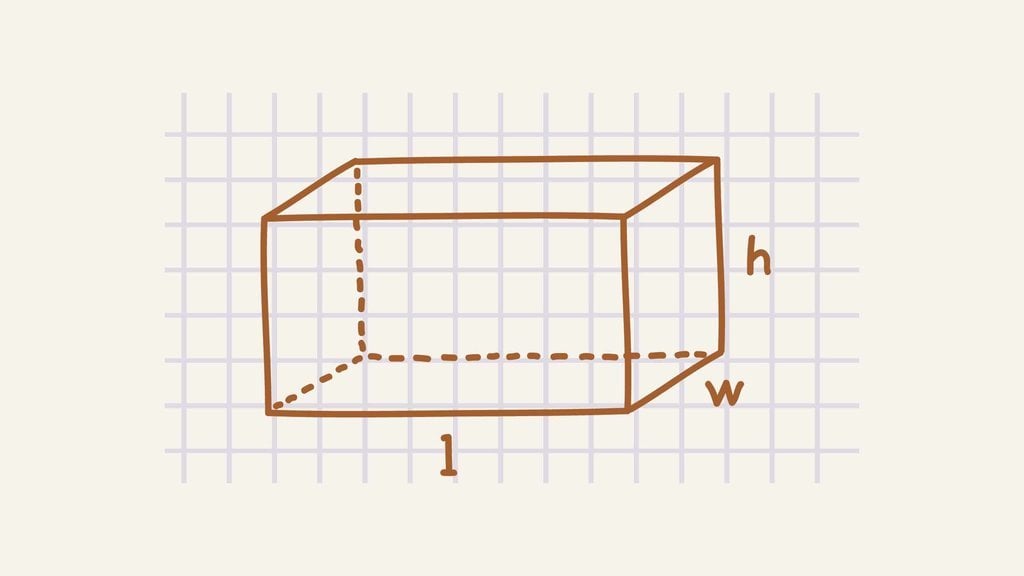
Prisma segi empat adalah bangun ruang tiga dimensi yang memiliki dua sisi berbentuk segi empat yang kongruen pada bagian alas dan tutupnya. Prisma segi empat juga sering disebut sebagai kubus atau balok. Adapun unsur unsur prisma segi empat antara lain:

1. Sisi/bidang

n+2 = 4 + 2 = 6

Jadi, prisma segi empat memiliki 6 buah sisi atau bidang.

2. Rusuk

3n = 3 x 4 = 12

Jadi, prisma segi empat memiliki 12 buah rusuk.

3. Titik sudut

2n = 2 x 4 = 8

Jadi, prisma segi empat memiliki 8 buah titik sudut.

4. Diagonal sisi

n(n-1) = 4(4-1) = 12

Jadi, prisma segi empat memiliki 12 buah diagonal sisi.

5. Diagonal ruang

n(n-3) = 4(4-3) = 4

Jadi, prisma segi empat memiliki 4 diagonal ruang.

6. Bidang diagonal

n/2 x (n-1) = 4/2 x (4-1) = 6

Jadi, prisma segi empat memiliki 6 bidang diagonal

Prisma Segi Lima

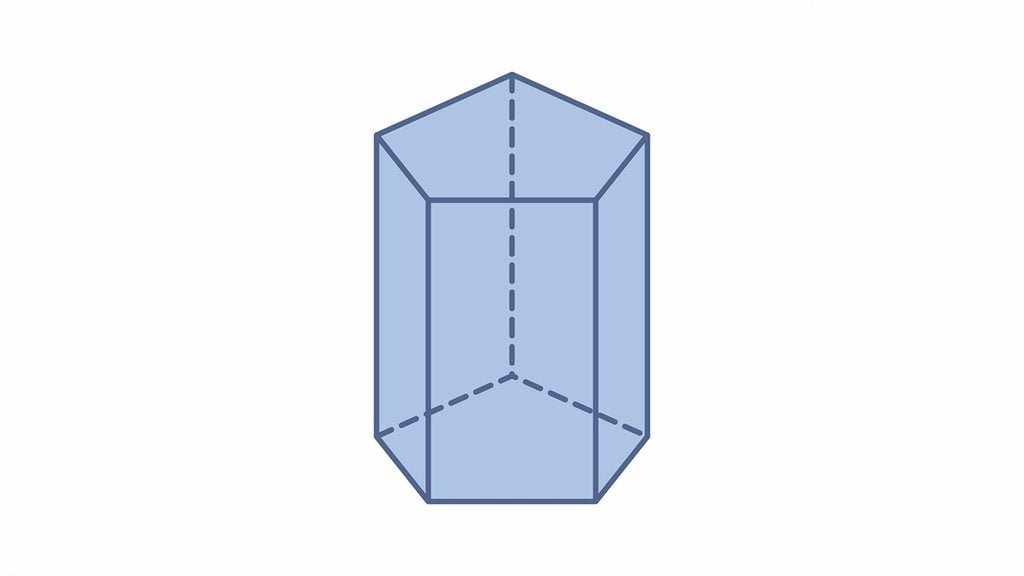
Prisma segi lima merupakan bangun ruang tiga dimensi yang memiliki alas dan tutup berbentuk segi lima atau pentagon. Adapun unsur unsur prisma segi lima antara lain:

1. Sisi/bidang

n+2 = 5 + 2 = 7

Jadi, prisma segi lima memiliki 7 buah sisi atau bidang.

2. Rusuk

3n = 3 x 5 = 15

Jadi, prisma segi lima memiliki 15 buah rusuk.

3. Titik sudut

2n = 2 x 5 = 10

Jadi, prisma segi lima memiliki 10 buah titik sudut.

4. Diagonal sisi

n(n-1) = 5(5-1) = 20

Jadi, prisma segi lima memiliki 20 buah diagonal sisi.

5. Diagonal ruang

n(n-3) = 5(5-3) = 10

Jadi, prisma segi lima memiliki 10 diagonal ruang.

6. Bidang diagonal

n/2 x (n-1) = 5/2 x (5-1) = 10

Jadi, prisma segi lima memiliki 10 bidang diagonal

Prisma Segi Enam

Prisma segi enam adalah bangun ruang tiga dimensi dengan alas dan tutup yang berbentuk segi enam serta sisi-sisi lain yang berbentuk persegi. Adapun unsur unsur prisma segi enam antara lain:

1. Sisi/bidang

n+2 = 6 + 2 = 8

Jadi, prisma segi enam memiliki 8 buah sisi atau bidang.

2. Rusuk

3n = 3 x 6 = 18

Jadi, prisma segi enam memiliki 18 buah rusuk.

3. Titik sudut

2n = 2 x 6 = 12

Jadi, prisma segi enam memiliki 12 buah titik sudut.

4. Diagonal sisi

n(n-1) = 6(6-1) = 30

Jadi, prisma segi enam memiliki 30 buah diagonal sisi.

5. Diagonal ruang

n(n-3) = 6(6-3) = 18

Jadi, prisma segi enam memiliki 18 diagonal ruang.

6. Bidang diagonal

n/2 x (n-1) = 6/2 x (6-1) = 15

Jadi, prisma segi enam memiliki 15 bidang diagonal

Mengetahui unsur unsur prisma sangat penting untuk memahami bangun ruang dan aplikasinya dalam kehidupan sehari-hari, misalnya untuk arsitektur dan desain produk. Hal ini juga membantu kita dalam perhitungan volume maupun luas permukaan, memungkinkan kita untuk merancang dan menciptakan objek-objek yang estetik dan fungsional.