15 Rumus Persamaan Trigonometri Lengkap dengan Penjelasannya

tirto.id - Kumpulan rumus trigonometri lengkap ini bisa jadi bahan belajar bagi para siswa yang sedang mempelajari materi trigonometri di kelas masing-masing.

Trigonometri ternyata bukan rumus sembarangan. Tercatat, trigonometri sempat digunakan oleh para pelaut kuno untuk menavigasi pelayaran mereka. Selain itu, trigonometri juga digunakan untuk membangun piramida di Mesir Kuno.

Poinnya, mempelajari rumus-rumus trigonometri adalah bukan hal yang sia-sia. Selain sangat bermanfaat, bila sudah tahu triknya, mempelajari trigonometri bisa jadi hal yang sangat menyenangkan.

Namun, sebelum melihat rumus trigonometri lengkap, tampaknya perlu diketahui terlebih dahulu mengenai pengertian trigonometri itu sendiri.

Apa Itu Trigonomteri?

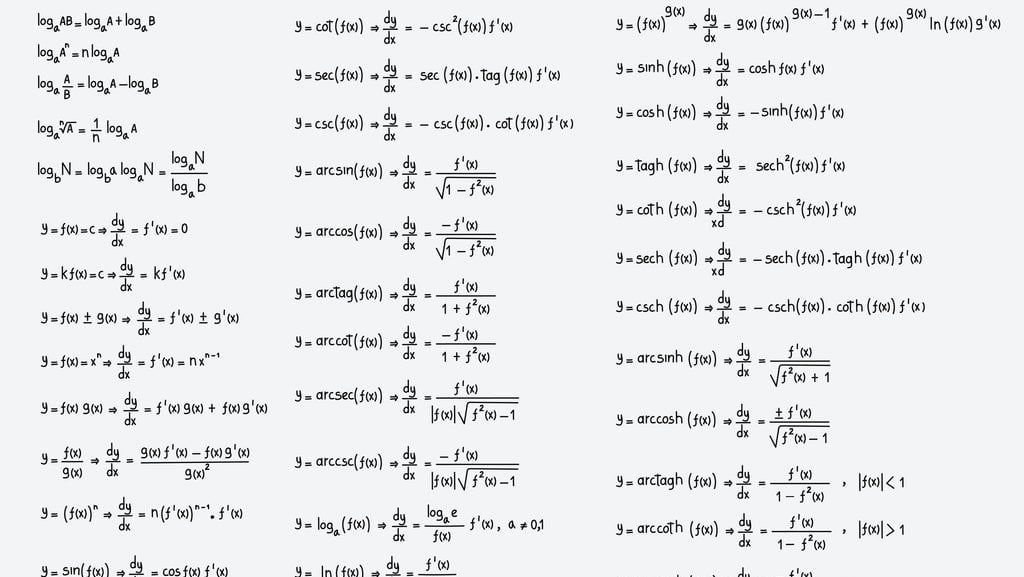
Trigonometri adalah kata yang berasal dari bahasa Yunani, "trigonon" atau "tiga sudut" dan "metron" yang berarti “mengukur”. Cabang ilmu matematika ini mempelajari hubungan antara sisi dan sudut dalam sebuah segitiga.

Hubungan ini biasanya dinyatakan dalam bentuk perbandingan sinus, kosinus, dan tangen. Dengan menggunakan perbandingan ini, ukuran panjang sisi segitiga dapat dengan mudah diukur, meskipun hanya mengetahui panjang satu sisi dan sudutnya saja.

Materi trigonometri ini umumnya sudah diajarkan sejak kelas 10 di Sekolah Menengah Atas (SMA). Dengan mengajarkan materi ini, para guru berharap para siswa bisa menerapkannya dalam kehidupan sehari-hari mereka karena ilmu trigonometri punya banyak manfaat.

Beberapa manfaat dari trigonometri itu di antaranya adalah mulai dari bidang astronomi, teknik sipil, geografi, oseanografi, arsitektur, fisika, kesehatan, penentuan waktu salat, dan masih banyak lainnya.

Kumpulan Rumus Persamaan Trigonometri Lengkap

Berikut ini kumpulan rumus trigonometri lengkap yang bisa dipelajari dan dicermati oleh para siswa yang sedang mempelajari ilmu trigonometri.

Perlu diketahui bahwa rumus paling dasar dalam trigonometri melibatkan definisi fungsi-fungsi dasar trigonometri. Berbagai fungsi dasar trigonometri tersebut dinyatakan sebagai perbandingan sisi-sisi segitiga siku-siku.

Rumus Dasar Trigonometri

Rumus dasar trigonometri itu di antaranya adalah:

1. Sinus (sin)

sin α = panjang sisi depan/panjang sisi miring

2. Cosinus (cos)

cos⁡ α = panjang sisi samping/panjang sisi miring

3. Tangen (tan)

tan⁡ α = panjang sisi depan/panjang sisi samping

4. Kosekan (cosec)

csc⁡ α = 1/sin α= panjang sisi miring/panjang sisi depan

5. Sekan (sec)

sec⁡ α = 1/cos⁡ α= panjang sisi miring/panjang sisi samping

6. Kotangen (cot)

cot⁡ α = 1/tan α= panjang sisi samping/panjang sisi depan

Rumus-rumus dasar trigonometri ini mendasarkan pada definisi dasar trigonometri dalam konteks segitiga siku-siku. Pada rumus tersebut α merupakan sudut dalam segitiga siku-siku tersebut.

Lantas, bagaimana dengan trigonometri sudut istimewa?

Rumus Trigonometri Sudut Istimewa

Segitiga sudut istimewa merupakan segitiga yang memiliki nilai sudut dan sisi yang ukurannya tepat dan pasti. Inilah yang membuat segitiga sudut istimewa ini sering digunakan dalam perhitungan trigonometri.

Segitiga dengan sudut istimewa ini salah satunya disebut sebagai segitiga sama sisi yang memiiki jumlah sudut total 180 derajat, dengan setiap sudut berukuran 60° derajat. Selain itu ada juga persegi yang memiliki empat sudut. Masing-masing sudut berbentuk segitiga itu besarnya 90° derajat.

Dari bentuk-bentuk segitiga dasar tersebut, dapat dibangun segitiga-segitiga dengan sudut istimewa, seperti 30°, 45°, dan 60°. Jika segitiga sama sisi dibagi menjadi dua bagian, maka akan didapatkan segitiga dengan sudut 30°, 60°, dan 90°. Sedangkan, jika persegi dibagi secara diagonal, maka akan didapatkan segitiga dengan sudut 45°, 45°, dan 90°.

Rumus Identitas Trigonometri

Untuk memahami rumus identitas trigonometri perlu dipahami tentang identitas trigonometri. Identitas trigonometri sendiri adalah suatu pernyataan matematis yang menunjukkan kesetaraan antara dua ekspresi trigonometri.

Identitas trigonometri ini memungkinkan seseorang mengubah atau menjelaskan satu fungsi trigonometri di sisi kiri atau kanan persamaan. Pada akhirnya, persamaan itu akan menghasilkan bentuk akhir yang sama dengan sisi lainnya.

Contoh rumus identitas trigonometri adalah: tan α + cot α = sec α . csc α

Penjelasan dari rumus tersebut adalah, sisi kiri menunjukkan penjumlahan dari fungsi tangen (tan α) dan kotangen (cot α), sementara sisi kanan merupakan hasil dari perkalian fungsi sekannya (sec α) dan kosekannya (csc α).

Agar lebih jelas berikut ini berbagai rumus identitas trigonometri dalam materi trigonometri:

1. Rumus Identitas Trigonometri Sudut Ganda

• sin(2α) = 2sin(α) cos(α)
• cos(2α)= cos²(α)−sin²(α) = 1 − 2sin²(α) = 2cos²(α) − 1
• tan(2α)= 2tan(α)/ 1 − tan²(α)

2. Rumus Identitas Trigonometri Ganjil Genap

• sin (-α) = -sin α
• cos (-α) = cos α
• tan (-α) = -tan α

3. Rumus Identitas Trigonometri Setengah Sudut

• sin ½α = ± √(1 ‒ cos α)/2)
• cos ½α = ±√(1 + cos α)/2)
• tan ½α = ±√(1 ‒ cos α)/(1 + cos α) tan ½α = sin α/(1 + cos α) tan ½α = √(1 ‒ cos α)/ sin α

4. Rumus Identitas Trigonometri Kofungsi

• sin (π/2 − α)= cos(α)
• cos (π/2 − α)= sin(α)
• tan (π/2 − α)= cot(α)

5. Rumus Identitas Trigonometri Pythagoras

• sin²(α) + cos² (α) = 1
• 1 + tan² (α) = sec²(α)
• 1 + cot² (α) = csc²(α)

6. Rumus Identitas Trigonometri Jumlah dan Selisih Dua Sudut

• sin (α + β) = sin(α) cos(β) + cos(α) sin(β)
• sin (α − β) = sin(α) cos(β)− cos(α) sin(β)
• cos (α + β) = cos(α) cos(β) − sin(α) sin(β)
• cos (α − β) = cos(α) cos(β) + sin(α) sin(β)
• tan (α + β) = tan(α) + tan(β) / 1 − tan(α) tan(β)
• tan (α − β) = tan(α) − tan(β) / 1 + tan(α) tan(β)

7. Rumus Identitas Trigonometri Perkalian Fungsi Trigonometri Sinus dan Cosinus

• sin α sin β = -1/2 (cos(α+β) – cos(α-β))
• cos α cos β = 1/2 (cos(α+β) + cos(α-β))
• sin α cos β = 1/2 (sin(α+β) + sin(α-β))
• cos α sin β = 1/2 (sin(α+β) – sin(α-β))

8. Rumus Identitas Trigonometri Jumlah dan Selisih Fungsi Trigonometri Sinus dan Cosinus

• sin α + sin β = 2 sin ((α+β)/2) cos ((α-β)/2)
• sin α – sin β = 2 cos ((α+β)/2) sin ((α-β)/2)
• cos α + cos β = 2 cos ((α+β)/2) cos ((α-β)/2)
• cos α – cos β = -2 sin ((α+β)/2) sin ((α-β)/2)

Contoh Penerapan Trigonomteri dalam Kehidupan Sehari-hari

Rumus trigonometri ini ternyata sangat bermanfaat dalam kehidupan sehari-hari. Beberapa contoh penerapan rumus trigonometri dalam kehidupan sehari-hari yang mudah dijumpai di antaranya adalah:

Untuk Navigasi dan Pemetaan

Trigonometri digunakan dalam GPS dan sistem navigasi. Kedua hal ini mengaplikasikan berbagai prinsip trigonometri untuk menentukan posisi pengguna GPS berdasarkan sinyal dari satelit.

Salah satu yang sangat berjasa terhadap trigonometri adalah para pilot pesawat atau kapten kapal. Para profesional ini menggunakan trigonometri untuk menentukan arah dan jarak yang harus mereka tempuh.

Dalam Bidang Astronomi

Dalam bidang astronomi ini trigonometri digunakan untuk menghitung jarak bintang atau planet. Salah satu metode yang digunakan adalah metode paralaks.

Dengan metode paralaks ini astronom bisa menentukan jarak benda langit menggunakan prinsip segitiga dan sudut pengamatan dari dua titik di Bumi.

Dalam Bidang Arsitektur dan Konstruksi

Prinsip trigonometri kerap digunakan oleh tukang bangunan untuk menentukan sudut kemiringan atap. Hal ini perlu dilakukan agar air hujan bisa mengalir dengan baik.

Selain menghitung sudut kemiringan, trigonometri juga digunakan untuk menentukan tinggi bangunan tanpa harus memanjat. Tukang bangunan menggunakan sudut elevasi dan panjang bayangan untuk mengukur hal tersebut.

Untuk Pembuatan Musik Elektronik

Gelombang suara yang ditampilkan dalam bentuk sinus dan kosinus adalah hasil dari penerapan fungsi-fungsi trigonometri. Hal ini diaplikasikan secara praktis dalam pembuatan berbagai alat musik elektronik.

Bidang Olahraga

Dalam bidang olahraga digunakan oleh para atlet untuk mempertimbangkan sudut lemparan dan gaya agar hasilnya optimal. Selain itu, dalam bidang olahraga senam atau skateboard, para atletnya menggunakan konsep trigonometri untuk memperhitungkan sudut rotasi dan kecepatan.

Demikianlah kumpulan rumus trigonometri yang bisa digunakan oleh para siswa untuk mempelajari materi trigonometri secara mandiri di rumah masing-masing. Dengan belajar secara mandiri, materi trigonometri yang diberikan bisa lebih dipahami dan dikuasai oleh para siswa secara lebih baik.