tirto.id - Kumpulan contoh soal mata pelajaran matematika materi nilai mutlak kelas 10 dan pembahasannya ini bisa dijadikan referensi belajar, terutama bagi siswa kelas 10 sebagai bahan persiapan menghadapi ujian sekolah.
Nilai mutlak adalah salah satu materi dalam mata pelajaran Matematika yang harus dipelajari oleh siswa kelas 10. Dalam materi nilai mutlak, para siswa kelas 10 akan mempelajari bagaimana sesuatu itu tidak pernah bernilai negatif.
Penjelasan nilai mutlak ini akan dijabarkan dalam konsep dan fungsi nilai mutlak, persamaan dan pertidaksamaan linear nilai mutlak, hingga berbagai permasalahan yang berkaitan dengan nilai mutlak.
Sebagai bahan persiapan menghadapi ujian sekolah, khususnya mata pelajaran Matematika, materi nilai mutlak akan diuraikan secara singkat di bawah ini. Dipaparkan pula rangkuman materi nilai mutlak, serta berbagai contoh soal mengenai nilai mutlak yang bisa dijadikan bahan latihan.
Rangkuman Materi Nilai Mutlak Kelas 10
Dalam Matematika, terdapat konsep sesuatu yang tidak pernah bernilai negatif atau nilai bilangan yang sifatnya selalu positif. Hal ini disebut nilai mutlak. Oleh karena itu, bilangan positif maupun nol memiliki nilai mutlak dari bilangan itu sendiri. Adapun bilangan negatif, nilai mutlaknya merupakan lawan dari bilangan tersebut.
Nilai mutlak bilangan 3 ditulis |3| adalah 3 dan nilai mutlak bilangan -3 ditulis |-3| adalah 3. Nilai mutlaknya tidak pernah bernilai negatif, berapapun besar atau kecil nilai bilangan tersebut.
Pedoman membuat grafik fungsi nilai mutlak adalah sebagai berikut.
- Pertama-tama, buat tabel fungsi nilai mutlak untuk beberapa titik
- Isi tabel berisi fungsi nilai mutlak
- Masukkan titik dari tabel fungsi nilai mutlak ke dalam sistem koordinat cartesius
Sifat-sifat nilai mutlak pada persamaan nilai mutlak linear satu variabel meliputi:
|x| = √x²
|a . b| = |a|. |b|
ab = |a||b|, b ≠ 0
Persamaan linear satu variabel bisa dihitung menggunakan persamaan nilai mutlak yang diberikan. Sebagai contoh, apabila diketahui |ax + b| = c, untuk nilai a, b, dan c adalah bilangan real. Mengacu definisi nilai mutlak, maka didapatkan persamaan ax + b = c atau ax + b = -c.
Hanya persamaan nilai mutlak |ax + b| = c yang memiliki penyelesaian jika c ≥ 0.
Sifat pertidaksamaan nilai mutlak linear satu variabel:
- Apabila bilangan a ≥ 0 serta |x| ≤ a, sehingga berlaku –a ≤ x ≤ a untuk setiap bilangan a, b, x bilangan real
- Apabila bilangan a < 0 serta |x| ≤ a, sehingga tidak ada bilangan real x yang memenuhi pertidaksamaan nilai mutlak linear
- Apabila bilangan |x| ≥ 0 serta a > 0, sehingga berlaku x ≥ a atau x ≤ -a
- Berlaku aturan |a + b| ≤ |a| + |b| serta |a - b| ≥ |a| - |b|
Contoh Soal Nilai Mutlak dan Pembahasannya
Setelah membaca dan memahami rangkuman materi nilai mutlak, tahap berikutnya yang bisa dilakukan oleh siswa kelas 10 adalah mengerjakan berbagai soal mengenai nilai mutlak. Berikut ini kumpulan soal nilai mutlak kelas 10, beserta pembahasan yang bisa dijadikan bahan belajar untuk mempersiapkan ujian.
1. Tentukan nilai x dari |3x+2|²+|3x+2|-2=0
Pembahasan:
Misal : |3x+2| = p
Maka,
3x+2|²+|3x+2|-2=0
p² + p – 2 = 0
(p+2) (p-1) = 0
p+2 = 0
p = -2 (nilai mutlak tidak negatif )
atau
p-1 = 0
p = 1
|3x+2| = 1
=> 3x+2 = 1
3x = 1-2
3x = -1
x = -1/3
=> -(3x+2) = 1
3x+2 = -1
3x = -1-2
3x = -3
x = -1
Jadi, penyelesaiannya adalah x=-1/3 atau x=-1
2. Tentukanlah HP |2x – 1| = |x + 4|
Pembahasan:
|2x – 1| = |x + 4|
2x – 1 = x + 4 ataupun 2x – 1 = -(x + 4)
x = 5 ataupun 3x = -3
x = 5 ataupun x = -1
Maka, HP = (-1, 5)
3. Tentukanlah himpunan penyelesaian |4x + 2| ≥ 6
Pembahasan:
|4x + 2| ≥ 6 (4x + 2 ≤ -6 atau 4x + 2 ≥ 6)
|4x + 2| ≥ 6 (4x ≤ -8 atau 4x ≥ 4)
|4x + 2| ≥ 6 (x ≤ -2 atau x ≥ 1)
Maka, HP = (x ≤ -2 atau x ≥ 1)
4. Tentukanlah himpunan penyelesaian |2x – 7| = 3
Pembahasan:
|2x – 7| = 3 ( 2x – 7 = 3 ataupun 2x – 7 = -3)
|2x – 7| = 3 ( 2x = 10 ataupun 2x = 4)
|2x – 7| = 3 ( x = 5 ataupun x = 2)
Maka, HP = 2, 5
5. Tentukanlah himpunan penyelesaian dari |2x – 1| < 7
Pembahasan:
|2x – 1| < 7 (-7 < 2x – 1 < 7)
|2x – 1| < 7 (-6 < 2x < 8)
|2x – 1| < 7 (-3 < x < 4)
Maka, HP = (-3 < x < 4)
6. Tentukan penyelesaian dari |x-2|=3
Pembahasan:
|x-2|=3
===> x-2 = 3
x = 3+2
x = 5
===> -(x-2) = 3
x-2 = -3
x = -3+2
x = -1
Sehingga penyelesaiannya x=5 atau x=-1
7. Tentukan nilai x yang memenuhi |2x+16|=x+4
Pembahasan:
|2x+16|
===> 2x+16 untuk 2x+16 ≥ 0
2x ≥ -16
x ≥ -16/2
x ≥ -8
===> -(2x+16) untuk 2x+16 < 0
2x < -16
x < -16/2
x < -8
====>Untuk interval x≥-8
|2x+16| = x+4
2x+16 = x+4
2x-x = 4-16
x = -12
x=-12 tidak termuat dalam interval x≥8
Jadi interval x≥8 tidak mempunyai penyelesaian.
====>Untuk interval x<-8
|2x+16| = x+4
-(2x+16) = x+4
-2x-16 = x+4
-2x-x = 4+16
-3x = 20
x = 20/-3
x = -6 2/3
x=-6 2/3 tidak termuat dalam interval x<-8
Jadi interval x<-8 tidak mempunyai penyelesaian.
8. Tentukan penyelesaian dari |x-2| = |6+2x|
Pembahasan:
|x-2| = |6+2x|
(x-2)² = (6+2x)²
x²-4x+4 = 36+24x+4x²
0 = 4x²-x²+24x+4x+36-4
0 = 3x²+28x+32
0 = (3x+4) (x+8)
3x+4 = 0
3x = -4
x = -4/3
atau
x+8 = 0
x = -8
Sehingga penyelesaiannya x=-4/3 atau x=-8
9. Tentukan |𝑥 + 2| untuk 𝑥 bilangan real dengan menggunakan definisi nilai mutlak!
Pembahasan:

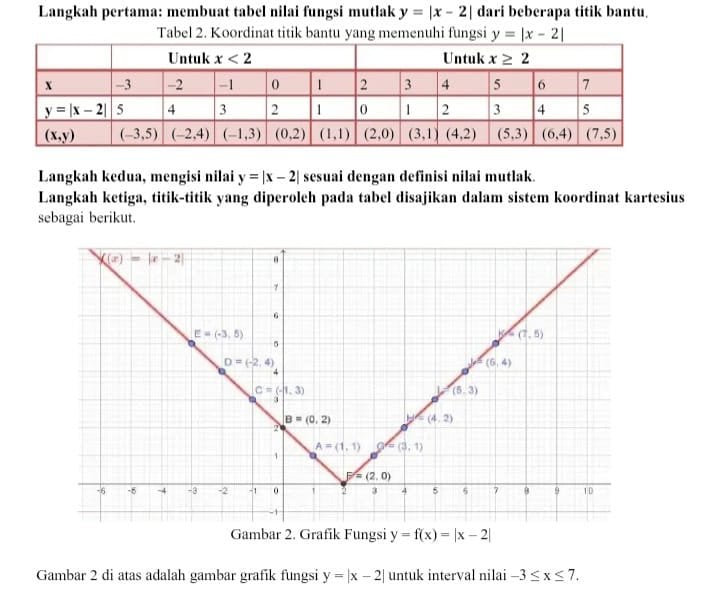
10. Gambarlah grafik 𝑦 = |𝑥 – 2|.
Pembahasan:
11. Tentukan penyelesaian |3x – 2| ≥ |2x + 7|
Pembahasan:
|3x – 2| ≥ |2x + 7|
⇔ 3x – 2 ≤ -(2x + 7) ataupun 3x – 2 ≥ 2x + 7
⇔ 5x ≤ -5 ataupun x ≥ 9
⇔ x ≤ -1 atau x ≥ 9
Maka, HP = (x ≤ -1 atau x ≥ 9)
12. Pada musim penghujan beberapa waktu lalu, telah terjadi kenaikan debit air di Sungai Citarum. Ambang batas normal debit air di sungai tersebut berkisar 400 m3/detik, sebagai acuan untuk menentukan status kewaspadaan banjir di sungai itu.
Tentukan fungsi nilai mutlak peningkatan dan penurunan debit air tersebut dengan perubahan dalam liter/detik.
Pembahasan:
Misalkan: 𝑥 adalah debit air sungai
Ambang batas normal debit air = 400 m3/detik.
Maka fungsi nilai mutlak peningkatan dan penurunan debit air tersebut dengan perubahan dalam liter/detik adalah: 𝑓(𝑥) = 𝑦 = |𝑥 – 400|
Editor: Ahmad Yasin & Yulaika Ramadhani












