Rangkuman Materi Bilangan Berpangkat Kelas 9 Kurikulum Merdeka

tirto.id - Materi bilangan berpangkat kelas 9 adalah salah satu topik penting dalam pelajaran matematika untuk siswa kelas 9. Materi ini biasanya dipelajari untuk memahami konsep eksponen dan penerapannya dalam berbagai soal. Artikel ini bertujuan untuk memberikan rangkuman yang mudah dipahami agar siswa bisa belajar mandiri di rumah.

Bilangan berpangkat juga dikenal dengan istilah eksponen, yang berarti perkalian berulang dari suatu bilangan. Misalnya, bilangan berpangkat 2² berarti 2 dikalikan dengan dirinya sendiri sebanyak dua kali. Contoh lainnya adalah 5⁴ yang berarti 5 dikalikan sebanyak empat kali, yaitu 5 x 5 x 5 x 5.

Dalam matematika, bilangan bisa berupa bilangan positif, negatif, atau pecahan yang memiliki aturan berbeda dalam perpangkatan. Oleh karena itu, siswa kelas 9 perlu memahami sifat-sifat bilangan berpangkat secara mendalam. Dengan memahami konsep ini, siswa dapat mengerjakan soal-soal eksponen dengan lebih mudah dan tepat.

Rangkuman Materi Bilangan Berpangkat Kelas 9 Kurikulum Merdeka

Untuk memudahkan belajar dan memahami keseluruhan materi, berikut rangkuman materi bilangan berpangkat untuk kelas 9:

A. Pengertian Bilangan Berpangkat

Pengertian bilangan berpangkat adalah bilangan yang dikalikan dengan bilangan itu sendiri hingga beberapa tingkat sebanyak jumlah pangkatnya.

Bentuk bilangan berpangkat adalah aⁿ

a = bilangan

n = pangkat

Contoh bilangan berpangkat: 3³ = 3 x 3 x 3

B. Bilangan Negatif Berpangkat

Perkalian berulang tetap berlaku pada bilangan negatif yang dipangkatkan.

Contoh:

-2² = -2 x -2 = 4

-2³ = -2 x -2 x -2 = -8

Kesimpulan: bilangan negatif dengan pangkat bilangan genap akan menghasilkan bilangan positif, sedangkan bilangan negatif dengan pangkat bilangan ganjil akan menghasilkan bilangan negatif.

C. Bilangan Berpangkat Negatif

Bilangan berpangkat negatif berarti bilangan tersebut dipangkat dengan bilangan negatif. Bilangan berpangkat negatif diartikan dengan satu per perkalian berulang suatu bilangan sebanyak jumlah pangkatnya.

Contoh:

2⁻³ = 1/2³ = 1 / 2 x 2 x 2 = 1/8

Kesimpulan: pangkat negatif menjadi positif dan berpindah posisi menjadi bilangan penyebut dalam pecahan

D. Sifat Bilangan Berpangkat

Berikut adalah rangkuman sifat-sifat perpangkatan kelas 9, sebagai berikut: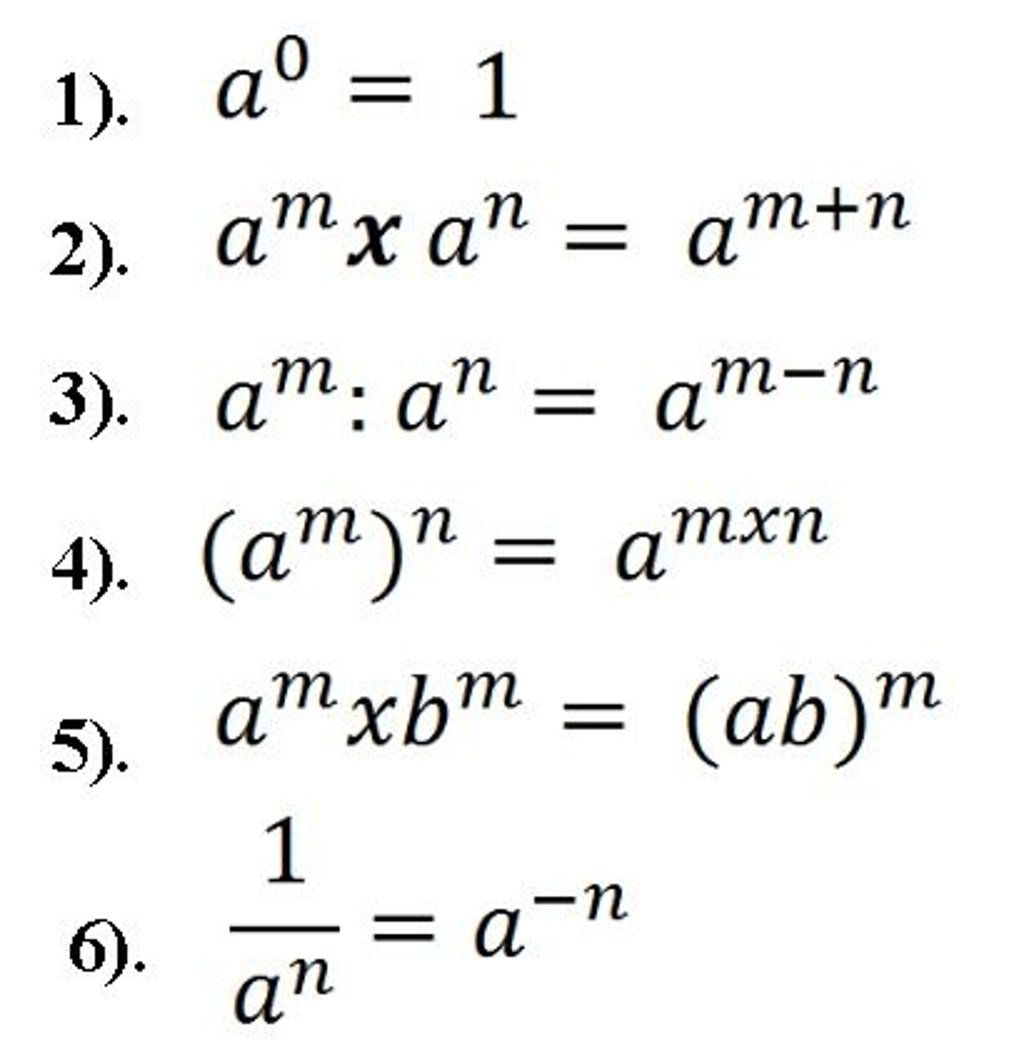

Pada sifat 1, bilangan berpangkat nol hasilnya selalu 1

Contoh sifat 2:

4² x 4³ = 4²⁺³ = 4⁵

4⁻² x 4⁻³ = 4⁽⁻²⁾⁺⁽⁻³⁾ = 4⁻⁵

4² x 4⁻³ = 4⁽²⁾⁺⁽⁻³⁾ = 4⁻¹

Contoh sifat 3:

4² : 4³ = 4²⁻³ = 4⁻¹

4⁻² : 4⁻³ = 4⁽⁻²⁾⁻⁽⁻³⁾ = 4¹

4² : 4⁻³ = 4⁽²⁾⁻⁽⁻³⁾ = 4⁵

Contoh sifat 4:

(4²)³ = 4⁶

(4⁻²)³ = 4⁻⁶

(4²)⁻³ = 4⁻⁶

Contoh sifat 5:

2² x 3² = (2 x 3)² = 6²

-2² x 3² = (-2 x 3)² = -6²

Contoh sifat 6: 1/2³ = 2⁻³

E. Bentuk Pangkat dalam Pecahan

Contoh:

(2/3)² = 2²/ 3²

(2/3)⁻² = 3²/2²

F. Rumus Bilangan Berpangkat

Operasi pangkat ini sangat penting dalam matematika karena memudahkan penulisan dan perhitungan bilangan yang berulang kali dikalikan. Dengan memahami rumus-rumus bilangan berpangkat, kita bisa menyelesaikan berbagai masalah matematika secara lebih efisien dan sistematis, seperti:

1. Perkalian dengan Basis yang Sama

A pangkat m X A pangkat n = A pangkat m+n

2. Pembagian dengan Basis yang Sama

A pangkat m : A pangkat n = A pangkat m-n

3. Pangkat dari Pangkat

(A pangkat m)n = A pangkat m x n

4. Pangkat dari Hasil Perkalian

(AB) pangkat n = A pangkat n X B pangkat n

5. Pangkat dari Hasil Pembagian

(A/B) pangkat n = A pangkat n / b pangkat n

Ingin mempelajari modul lainnya seputar matematika dan pelajaran menarik lainnya? Kunjungi artikel lengkapnya di Tirto.id melalui tautan di bawah ini.

Kumpulan Artikel tentang Materi Ajar