tirto.id - Contoh soal Olimpiade Komputer dan kunci jawabannya bisa dijadikan materi untuk latihan dan mempersiapkan diri jelang pelaksanaan OSN SMA 2024.
Olimpiade Sains Nasional (OSN) 2024 diselenggarakan oleh Balai Pengembangan Talenta Indonesia (BPTI). Ajang adu talenta siswa-siswi berprestasi digelar rutin setahun sekali.
OSN SMA/MA/sederajat 2024 bidang sains berlangsung secara bertingkat mulai level daerah hingga nasional. Tujuannya menjaring peserta terbaik dari setiap provinsi di Indonesia.
OSN SMA 2024 menggelar berbagai lomba cabang keilmuan yang masuk dalam bidang Riset dan Inovasi. Salah satunya adalah Informatika atau Komputer.
Kisi-Kisi Materi Informatika/Komputer OSN SMA 2024
Berdasarkan buku "Silabus Olimpiade Komputer Internasional untuk Seleksi Olimpiade Sains Nasional Tingkat Kabupaten/Kota, Provinsi, dan Nasional", berikut adalah daftar kisi-kisi materi Informatika atau Komputer OSN SMA 2024:
1. Materi analitika yang bersifat logika.
Tujuannya untuk menguji potensi akademis (skolastik) peserta, namun memiliki relevansi yang tinggi dengan problem solving dan elemen penting dalam menguasai pemrograman komputer.
2. Materi analitika yang bersifat aritmatik.
Materi ini sebenarnya sejalan dengan analitika dan logika. Soal aritmatika bukan sekedar menguji keterampilan dalam hitung-menghitung, tetapi juga cara berpikir yang logis dan analitis dengan soal bertemakan aritmatika.
3. Materi algoritmika.
Tujuannya guna menguji kemampuan peserta dalam memahami dan menyusun suatu algoritma. Aspek-aspek yang terkait dengan pengetahuan dan bahasa pemrograman direduksi seminimal mungkin ke tingkat pseudocode.
Ketiga kategori tersebut dapat diperjelas lewat penjabaran ke dalam beberapa aspek seperti berikut ini:
A. Tipe soal untuk menguji deskripsi soal.
Soal berbentuk cerita untuk menguji kemampuan aspek pertama dan kedua dari proses berpikir. Soal dibuat untuk mengukur algoritma dalam cerita, deduksi berdasarkan input yang menghasilkan output, deduksi berdasarkan tets case menghasilkan pemahaman proses, menemukan kasus-kasus ekstrim, optimasi, dan menemukan model matematika dari soal.
B. Tipe soal pemahaman algoritma.
Peserta harus memahami algoritma yang diberikan dalam notasi pseudopascal dan menelusuri eksekusi algoritma. Soal dibuat untuk mengukur konsep elemen konstruksi, algoritma secara menyeluruh, mengeksekusi dan proses tracing, serta mengkonstruksi (coding).
C. Tipe soal kemampuan dasar logika.
Berbagai pertanyaan logika terkait dengan aspek-aspek implikasi, 'jika dan hanya jika', kalkulus proposisi, dan induksi-deduksi.
D. Tipe soal kemampuan dasar aritmatika.
Sejumlah aspek aritmatika yang akan dipersoalkan adalah berisi unsur langka-langkah komputasi, kemampuan menyusun model matematik, sifat deret bilangan, dan penyusunan model keterkaitan (graf).
E. Tipe soal kemampuan dasar penunjang.
Jenis-jenis pertanyaan yang akan muncul adalah himpuna, aljabar logika, sifat bilangan (deret), finite state machine, dan kombinatorik.
F. Tipe soal lainnya yang relevan dengan potensi akademis.
Soal-soal yang relevan dalam pengujian potensi akademis dan 'computational thinking' yang tidak dikategorikan dalam tipe-tipe soal di atas.
Kumpulan Soal Olimpiade Komputer OSN SMA 2024 dan Jawabannya
Berikut ini adalah kumpulan soal Informatika atau Komputer untuk OSN SMA 2024 dan jawabannya:
1. Gambar sebagai berikut adalah peta jalan antar kota di negeri 1001 Malam.
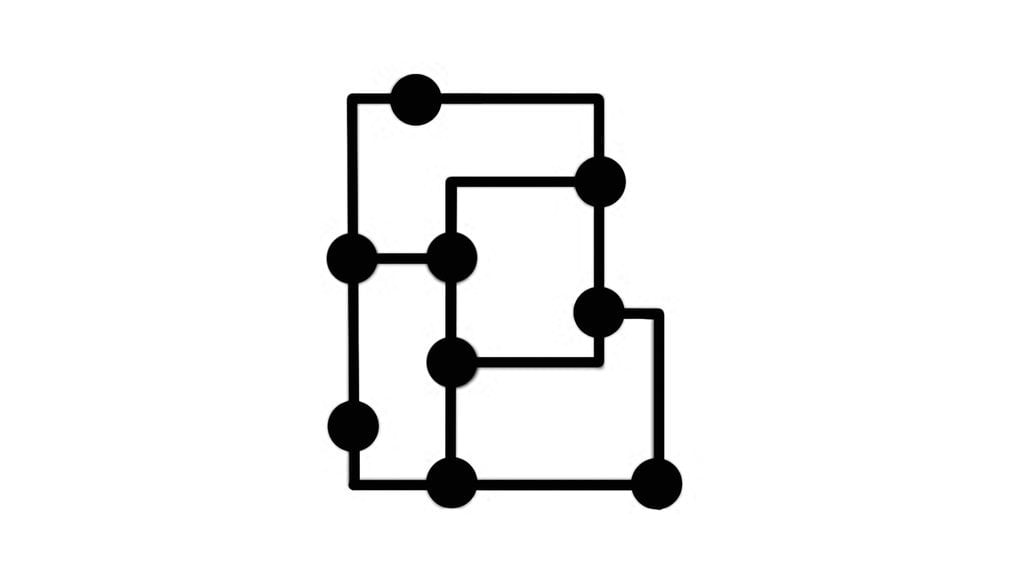
Sebuah jalan tambahan yang dibangun hanya dapat menghubungkan tepat dua buah kota, dan dua buah kota dapat dihubungkan oleh lebih dari 1 (satu) jalan. Berapakah minimum banyak jalan tambahan yang perlu dibangun agar seorang wisatawan yang berawal dari sebuah kota dapat menggunakan setiap jalan antar kota tepat sekali (tidak harus kembali ke kota asal)?
Jawaban: 2
Penjelasan:
Diperlukan pemahaman soal konsep graph untuk menyelesaikan soal ini. Permasalahan ini dapat dimodelkan sebagai berikut: “Ada berapa edge yang perlu ditambah agar terdapat eulerian path dari graph tersebut?".
Suatu graph dapat memiliki suatu eulerian path jika dan hanya jika banyak node yang memiliki degree ganjil tidak lebih dari 2 (perhatikan bahwa tidak mungkin terdapat graph yang memiliki banyaknya node dengan degree ganjil sebanyak 1). Perlu ditambahkan sesedikit mungkin edge agar syarat tersebut terpenuhi.
Dari gambar didapatkan ada 6 node yang memiliki degree ganjil. Hubungkan 4 node diantaranya dengan 2 edge agar jumlah node yang memiliki degree ganjil tinggal 2. Dengan demikian jawaban dari soal ini adalah 2.
2. Pada suatu hari, terdapat seekor semut yang terperangkap di dalam sebuah kaleng yang terbuka. Semut tersebut mula-mula berada pada posisi awal yaitu titik A, dan ingin mencapai titik keluar (titik B) seperti pada gambar dengan merayap pada dinding kaleng.
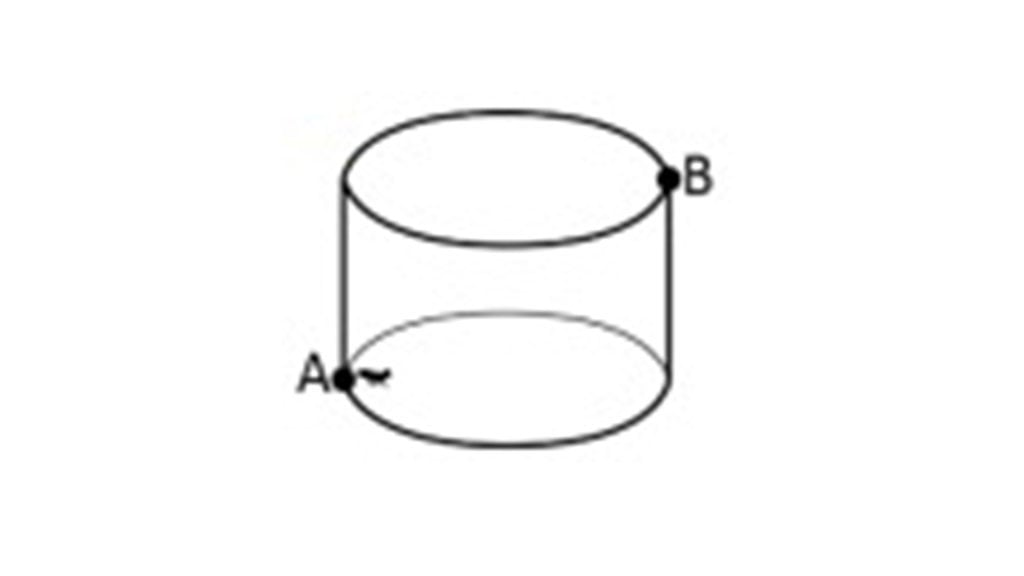
Jika diketahui jari-jari kaleng adalah 7 cm dan tinggi kaleng adalah 15 cm, berapakah jarak minimum yang perlu ditempuh oleh semut tersebut dari titik A untuk mencapai titik B? Tuliskan hasil jawaban dalam bentuk π (pi) jika perlu.
Jawaban: 26,62
Penjelasan:
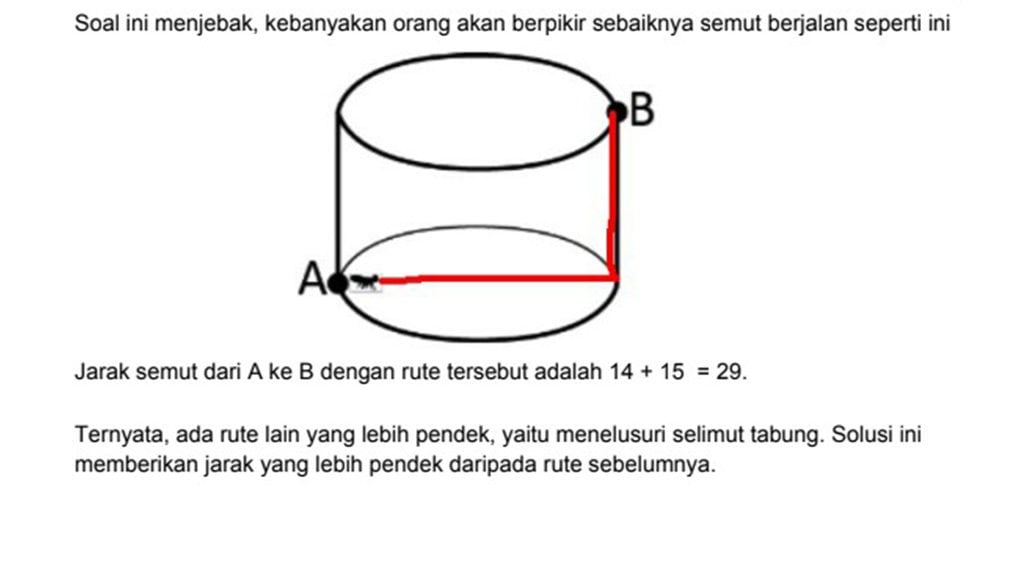
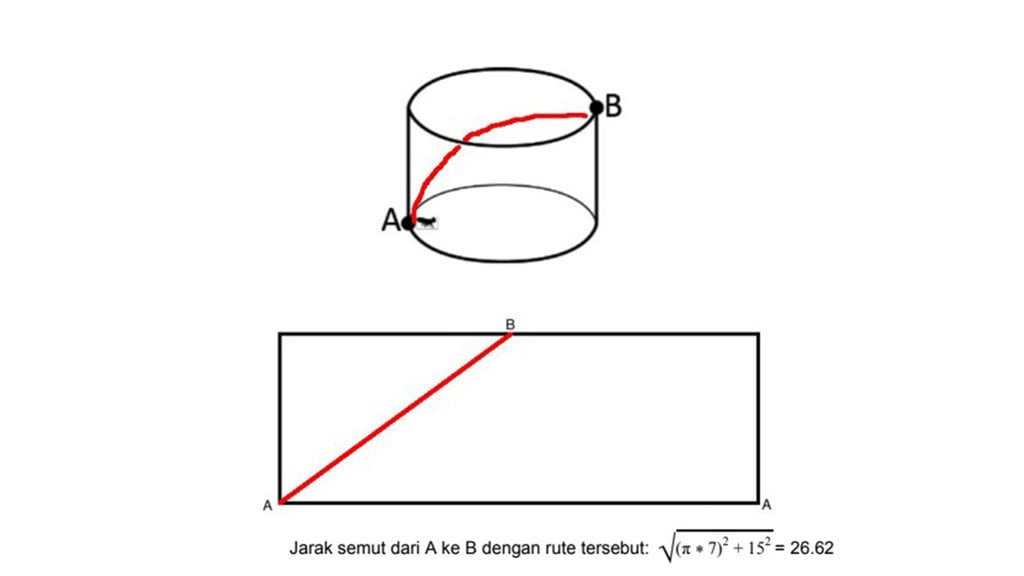
3. Pada sebuah arisan, jumlah orang yang hadir adalah 2016 orang, diberi identitas 1 sampai dengan 2016.Orang-orang tersebut akan dikelompokkan.
Orang ke-i akan ditaruh sekelompok dengan orang beridentitas i2 dan i3 kecuali jika i2 >2016 atau i3 > 2016. Tentukan berapa banyak kelompok yang ada pada arisan tersebut.
Jawaban: 1964
Penjelasan:
Banyak kelompok arisan adalah banyaknya bilangan yang bukan merupakan bilangan kuadrat atau kubik sempurna. Sebab, orang yang beridentitas berupa bilangan kuadrat atau kubik sempurna pasti dalam kelompoknya memiliki seorang teman yang identitasnya bukan bilangan kuadrat maupun kubik sempurna.

Perhatikan bahwa banyaknya kelompok harus ditambah 1, karena orang dengan identitas 1 tidak memiliki teman kelompok yang identitasnya bukan bilangan kuadrat atau kubik sempurna. Jadi, terdapat 1964 kelompok.
4. Pada sebuah pesta, terdapat 5 jenis pasangan makanan dan minuman yaitu jenis A, B, C, D, dan E. Setiap makanan jenis A, akan mempunyai pasangan minuman jenis A. Demikian juga untuk B, C, D, E.
Pak Dengklek mendapat kesempatan untuk mencicipi semua jenis makanan dan minuman. Namun, terdapat aturan bahwa setiap minuman jenis X hanya dapat diminum jika dan hanya jika makanan jenis X sudah dimakan. Sebagai contoh, minuman jenis A hanya dapat diminum apabila makanan jenis A sudah dimakan.
Berapa banyak kemungkinan urutan makan dan minum semua jenis makanan yang disediakan pada pesta tersebut? Anda dapat menuliskan jawaban dalam bentuk angka, atau dalam bentuk kombinasi, permutasi, dan faktorial.
Jawaban:
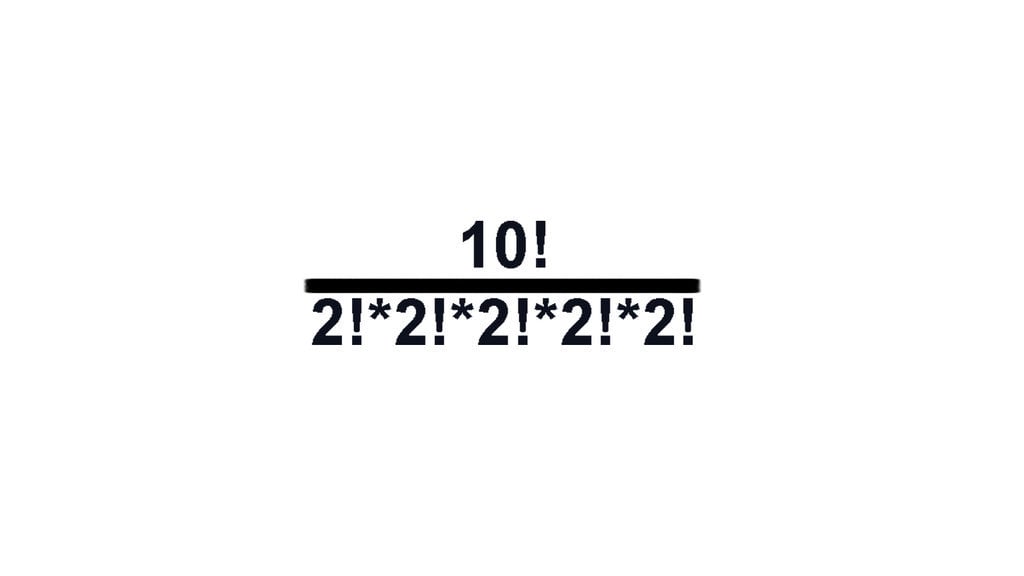
Penjelasan:
Banyak caranya adalah banyak permutasi dari AABBCCDDEE. Karena makanan harus didahulukan sebelum minuman, maka suatu makanan dan minuman “X” harus dilambangkan dengan huruf yang sama. Banyak permutasi adalah
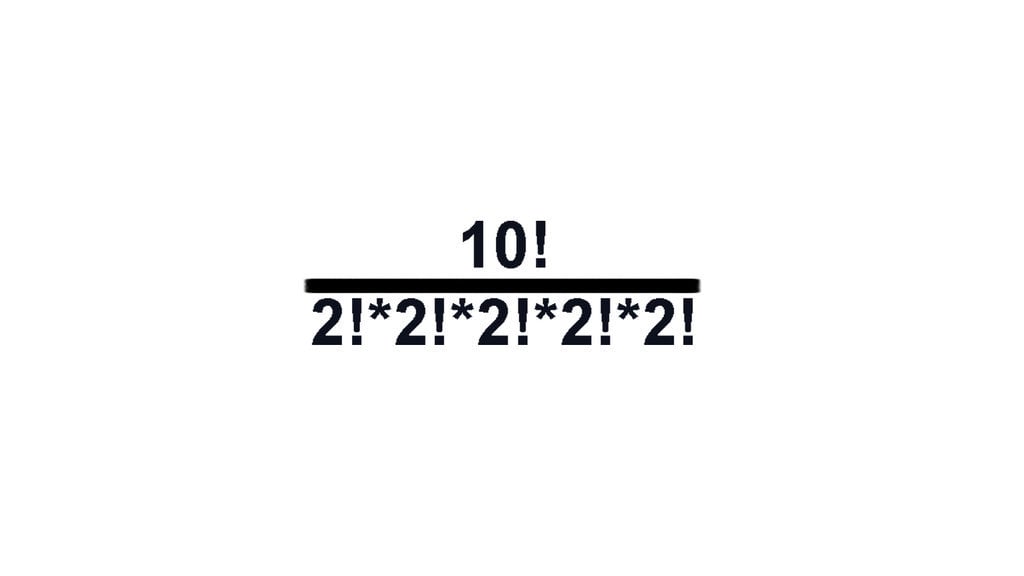
5. Diberikan sebuah larik (array) yang berisi 7 buah bilangan bulat yaitu: {42, 16, 40, 33, 0, 28, 41}. Pak Dengklek menginginkan sekumpulan bilangan (satu atau beberapa bilangan) yang jika dilakukan operasi XOR (exclusive-or terhadap representasi bit suatu bilangan) terhadap elemen-elemen larik tersebut satu demi satu, hasilnya adalah bernilai 0 (nol).
Pak Dengklek boleh menambahkan satu atau beberapa bilangan bulat ke dalam larik tersebut supaya keinginannya dapat tercapai. Namun ternyata, terdapat biaya yang perlu dibayar untuk menambahkan sekumpulan bilangan bulat, yaitu sebesar bilangan terbesar yang terdapat pada kumpulan bilangan tersebut.
Sebagai contoh, bilangan bulat yang ingin ditambahkan = {25, 17, 1} maka biaya yang perlu dibayar adalah 25. Berapakah biaya terkecil yang perlu dibayar Pak Dengklek? (Jika ternyata Pak Dengklek tidak perlu menambahkan apa-apa, tuliskan 0).
Jawaban: 0
Penjelasan:
Pak Dengklek tidak perlu menambahkan apapun karena sudah terdapat kumpulan bilangan yang menghasilkan nilai 0, yaitu {0}. Maka, jawabannya adalah 0.
6. Ada suatu negara yang bernama negara TOKI. Mata uang negara TOKI tersebut unik, yaitu berbentuk koinyang masing-masing bernilai 2n (1, 2, 4, 8, 16, .... s.d. 2048). Pak Dengklek ingin membeli suatu barang dengan harga 714 dan harus membayar dengan uang pas.
Berapa banyakkah pecahan mata uang minimum yang dibutuhkan untuk dapat membeli barang tersebut?
Jawaban: 5
Penjelasan:
Banyaknya pecahan mata uang yang diperlukan Pak Dengklek adalah sebanyak angka 1 pada representasi biner 714, yaitu (10 1100 1010)2. Terdapat 5 buah angka 1, sehingga minimum Pak Dengklek membutuhkan 5 koin.
7. Pak Dengklek adalah seseorang yang sangat suka dengan teka-teki. Pada suatu hari, ia membeli 10 bola, yangterdiri dari 3 warna putih, 4 warna merah, dan 3 warna hijau. Ia ingin mengambil beberapa bola tersebut secara bersamaan (boleh berapapun).
Berapa banyaknya bola minimum yang diperlukan, agar dapat dijamin bahwa pak Dengklek mengambil minimal 2 bola untuk setiap warna?
Jawaban: 8
Penjelasan:
Untuk menghitung minimal bola yang menjamin Pak Dengklek mengambil 2 bola untuk setiap warna, kita harus mencari kasus terburuk dari kejadian ini. Asumsikan Pak Dengklek sedang sangat tidak beruntung saat itu.
Berapa bola terbanyak yang dibutuhkan Pak Dengklek untuk mendapatkan 2 bola untuk tiap warna? Untuk kasus tersebut, bola yang diambil adalah: PPPMMMMHH. Sehingga, jawabannya adalah 8 bola.
8. Jika pernyataan “Persamaan matematika tersebut dibuat dengan kurang dari atau sama dengan 15 batang tusuk gigi.” diubah menjadi “Persamaan matematika tersebut dibuat dengan menggunakan tepat 15 batang tusuk gigi.”, berapa banyaknya string-persamaan-matematika berbeda yang dapat dibuat Pak Dengklek ?
Jawaban: 12
Penjelasan:
Berdasarkan tabel di nomor sebelumnya, kita hanya perlu menambahkan yang total batangnya tepat 15, sehingga terdapat 12 cara.
9. Apabila pada 1 hari dapat dilakukan > 1 rapat rutin untuk tim-tim yang tidak memiliki anggota yang sama, berapa hari minimal supaya sang pimpinan proyek dapat memastikan bahwa seluruh tim sudah melakukan rapat bulanan?
Jawaban: 5
Penjelasan:
Dari Tim I sampai Tim VI, hanya ada 2 pasangan tim yang dapat mengadakan rapat bersama, yaitu (Tim II - Tim III) dan (Tim III - Tim VI). Karena Tim II dan Tim VI tidak dapat mengadakan rapat bersama (Gogo berada pada kedua tim tersebut), kita hanya dapat mengambil 1 pasangan tim untuk rapat pada hari bersama.
Tanpa menghilangkan keumuman, kita ambil pasangan (Tim II - Tim III). Sisa tim harus rapat pada hari yang berbeda, sehingga perlu minimal 5 hari agar sang pimpinan proyek dapat memastikan bahwa seluruh tim sudah melakukan rapat bulanan.
10. Ternyata, terdapat sebuah modul proyek yang belum ditangani oleh tim I sampai VI sehingga sang pimpinan proyek membentuk sebuah tim kecil (tim VII) yang terdiri dari Abdul, Dono, dan Gogo. Berapa hari minimum supaya yang pimpinan proyek dapat memastikan bahwa tim I sampai VII sudah melakukan rapat bulanan?
Jawaban: 5
Penjelasan:
Perhatikan bahwa Tim VII dapat melakukan rapat pada hari yang sama dengan Tim V, sehingga hari yang diperlukan tetap sama, yaitu 5 hari.
Penulis: Lucia Dianawuri
Editor: Beni Jo & Yulaika Ramadhani
 Masuk tirto.id
Masuk tirto.id







































