15 Contoh Soal Pola Bilangan, Baris & Deret serta Kunci Jawaban

tirto.id - Kumpulan contoh soal pola bilangan, baris, dan deret beserta kunci jawabannya ini bisa dijadikan bahan latihan untuk menghadapi ujian atau ulangan. Ujian atau ulangan itu umumnya diadakan pada tengah atau akhir semester.

Pola bilangan, baris, dan deret adalah salah satu materi dalam mata pelajaran matematika Kelas 8 SMP atau MTs. Bahasan pola bilangan, baris, dan deret merupakan materi pertama yang dibahas dalam buku pelajaran matematika untuk Kelas 8.

Dengan mempelajari pola bilangan, baris, dan deret, para siswa dilatih untuk berpikir logis dan runtut sesuai dengan logika dasar matematika.

Untuk membantu para siswa kelas 8 mengingat kembali apa saja yang dipelajari dalam materi pola bilangan, baris, dan deret, rangkuman mengenai materi tersebut dapat dirujuk jika ingin mengasah materi bagian tersebut.

Rangkuman Materi Pola Bilangan, Baris, dan Deret

Berikut ini rangkuman materi pola bilangan, baris, dan deret sesuai dengan bahasan matematika yang diajarkan di Kelas 8.

1. Pengertian pola bilangan:

Pola bilangan adalah susunan angka-angka yang membentuk pola tertentu, misalnya segitiga, garis lurus, persegi, dan masih banyak lainnya.

2. Macam-macam pola bilangan:

a. Pola bilangan persegi panjang.

Pola bilangan jenis ini akan menghasilkan bentuk menyerupai persegi panjang. Contohnya susunan angka 2, 6, 12, 20, 30, dan seterusnya. Jika diuraikan, pola bilangannya berbentuk seperti berikut:

Pola 𝑘𝑒 − 𝑛 untuk persegi panjang : 𝑼𝒏 = 𝒏 𝒙 (𝒏 + 𝟏) 𝒂𝒕𝒂𝒖 𝑼𝒏 = 𝒏 (𝒏 + 𝟏)

b. Pola bilangan persegi.

Pola persegi adalah susunan bilangan yang dibentuk oleh bilangan kuadrat. Contoh susunan bilangan yang menghasilkan pola persegi adalah 1, 4, 9, 16, 25, 36, dst. Jika dijabarkan dalam bentuk gambar, maka akan menjadi seperti berikut:

Pola 𝑘𝑒 − 𝑛 untuk persegi : 𝑼𝒏 = 𝒏 𝒙 𝒏 = 𝒏2

c. Pola bilangan segitiga.

Bilangan juga dapat digambarkan melalui noktah yang mengikuti pola segitiga. Bilangan yang mengikuti pola segitiga dapat dituliskan sebagai berikut: 1, 3, 6, 10, 15, … (bilangan ini berasal dari penjumlahan bilangan cacah).

Pola 𝑘𝑒 − 𝑛 untuk segitiga : 𝑼𝒏 = 𝟏/𝟐 𝒙 𝒏 𝒙 (𝒏 + 𝟏) = 𝟏/𝟐 𝒏 (𝒏 + 𝟏)

d. Pola bilangan ganjil.

Pola bilangan ganjil memiliki aturan sebagai berikut. Bilangan 1 sebagai bilangan awal. Bilangan selanjutnya memiliki selisih 2 atau menambahkan 2 dengan bilangan sebelumnya. Bilangan ganjil memiliki pola: 1, 3, 5, 7, 9, …

Pola 𝑘𝑒 − 𝑛 untuk bilangan ganjil : 𝑼𝒏 = 𝟐 𝒙 𝒏 − 𝟏 = 𝟐𝒏 − 1

e. Pola bilangan genap.

Pola bilangan genap memiliki aturan sebagai berikut. Bilangan 2 sebagai bilangan awal. Bilangan selanjutnya memiliki selisih 2 atau menambahkan 2 dengan bilangan sebelumnya. Bilangan ganjil memiliki pola: 2, 4, 6, 8, …

Pola 𝑘𝑒 − 𝑛 untuk bilangan genap : 𝑼𝒏 = 𝟐 𝒙 𝒏 = 𝟐n

3. Barisan dan deret.

a. Barisan bilangan adalah susunan bilangan yang membentuk pola atau aturan tertentu, dan setiap anggota bilangan barisan disebut Suku. 𝑼𝟏,𝑼𝟐,𝑼𝟑,…..𝑼𝒏 Suku Pertama 𝑼𝟏, Suku Kedua 𝑼𝟐, dst

Contoh : Barisan 7, 14, 21, 28, …. 𝑼𝟏 = 𝟕, 𝑼𝟐 = 𝟏𝟒, 𝑼𝟑 = 𝟐𝟏, 𝑼𝟒 = 𝟐𝟖 , dst

b. Deret bilangan adalah bentuk penjumlahan dari suku-suku barisan tersebut.

Contoh : 𝑼𝟏+ 𝑼𝟐 + 𝑼𝟑+ 𝑼𝟒 … . + 𝑼𝒏, dst 7 + 14 + 21 + 28 + ⋯

4. Menentukan suku ke-n suatu barisan bilangan.

Menentukan suku ke-n suatu barisan bilangan sama artinya dengan menentukan rumus suku umum dari barisan bilangan tersebut.

a. Pola tingkat satu suatu barisan bilangan berselisih tetap.

Suatu barisan bilangan yang mempunyai selisih tetap pada tingkat pertama disebut pola tingkat satu suatu barisan bilangan berselisih tetap.

Rumus suku ke-n : 𝑼𝒏 = 𝒂𝒏 + 𝒃

dengan 𝒂 = 𝒔𝒖𝒌𝒖 𝒑𝒆𝒓𝒕𝒂𝒎𝒂 = 𝑼𝟏 𝒃 = 𝒃𝒆𝒅𝒂/𝒔𝒆𝒍𝒊𝒔𝒊𝒉

= 𝑼𝟐 − 𝑼𝟏 𝑎𝑡𝑎𝑢 𝑼𝟑 − 𝑼2

b. Pola tingkat dua suatu barisan bilangan berselisih tetap.

Suatu barisan bilangan yang mempunyai selisih tetap pada tingkat kedua disebut pola tingkat dua suatu barisan bilangan berselisih tetap.

Rumus suku ke-n : 𝑼𝒏 = 𝒂𝒏𝟐 + 𝒃𝒏 + c

5. Barisan dan deret aritmatika.

a. Barisan aritmatika adalah barisan bilangan yang selisih antara dua suku barisan yang berurutan nilainya selalu tetap atau sama. Selisih yang selalu tetap ini disebut "beda". Barisan aritmatika yang mempunyai beda positif (nilai suku-sukunya semakin membesar) disebut barisan aritmatika naik, sedangkan bedanya negatif (nilai suku sukunya semakin mengecil) disebut barisan aritmatika turun.

Contoh :

Contoh barisan aritmatika ➢ 2, 6, 10, 14, 18, 22, …

suku pertama: a = 2, beda : b = 4

rumus suku ke n: Un = 4n – 2

b. Deret Aritmatika adalah bentuk penjumlahan dari suku-suku pada sebuah barisan . Jika 𝑼𝟏,𝑼𝟐,𝑼𝟑,….. barisan aritmatika, maka 𝑼𝟏 + 𝑼𝟐 + 𝑼𝟑 + … adalah deret aritmatika.

Rumus Deret Aritmatika:

𝑺𝒏 = 𝒏/𝟐 (𝒂 + 𝑼𝒏) 𝒂𝒕𝒂𝒖 𝑺𝒏 = 𝒏/𝟐 (𝟐𝒂 + (𝒏 − 𝟏) 𝒃)

6. Barisan dan deret geometri.

Barisan geometri adalah barisan bilangan yang perbandingan setiap dua suku barisan yang berurutan nilainya selalu tetap atau sama. Perbandingan yang selalu tetap ini disebut Rasio.

Contoh :

a. Barisan 2, 4, 8, 16, 32, 64, … merupakan barisan geometri dengan rasio = 2, karena perbandingan setiap dua suku yang berurutan besarnya selalu sama yaitu 2.

4/2 = 8/4 = 18/8 = 32/16 = 64/32 = ⋯ = 2

b. Barisan 1.024, 512, 256, 128, 64, …. merupakan barisan geometri dengan rasio = 1/2. Karena perbandingan setiap dua suku yang berurutan besarnya selalu sama yaitu 1/2.

512/1.024 = 256/512 = 128/256 = 64/128 = ⋯ = 1/2

7. Deret geometri.

Deret geometri adalah penjumlahan dari suku-suku barisan geometri. Jika 𝑈1, 𝑈2, 𝑈3, … . ,𝑈𝑛−1,𝑈𝑛 membentuk barisan geometri, bentuk penjumlahan 𝑈1 + 𝑈2 + 𝑈3 + … . +𝑈𝑛−1 + 𝑈𝑛 disebut deret geometri.

Rumus deret geometri:

Sn = a (1 - r pangkat n)/1-r, untuk r < 1 atau Sn = a (r pangkat n -1)/r-1, untuk r > 1

Kumpulan Soal Materi Pola Bilangan, Baris, dan Deret serta Kunci Jawabannya

Setelah membaca rangkuman dari materi pola bilangan, baris dan deret, siswa dapat berlatih mengerjakan soal pola bilangan, baris dan deret untuk kelas 8. Berikut ini 15 contoh soal isian pola bilangan, baris, dan deret yang disertai dengan pembahasannya:

1. Tentukan pola ke-6 pada barisan persegi panjang ini!

Penyelesaian : 𝑼𝒏 = 𝒏 𝒙 (𝒏 + 𝟏) 𝒂𝒕𝒂𝒖 𝑼𝒏 = 𝒏(𝒏 + 𝟏)

𝑼𝟔 = 𝟔 𝒙 (𝟔 + 𝟏) = 𝟔 𝒙 𝟕 = 42

2. Tentukan pola ke-8 pada barisan persegi ini!

Penyelesaian : 𝑼𝒏 = 𝒏 𝒙 𝒏 = 𝒏 pangkat 2

𝑼𝟖 = 𝟖 pangkat 2 = 𝟔4

3. Tentukan pola ke-9 pada barisan segitiga ini!

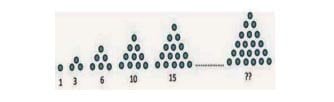
Penyelesaian : 𝑼𝒏 = 𝟏/𝟐 𝒙 𝒏 𝒙 (𝒏 + 𝟏) = 𝟏/𝟐 𝒏 (𝒏 + 𝟏)

𝑼𝟗 = 𝟏/𝟐 𝒙 𝟗 (𝟗 + 𝟏)

𝑼𝟗 = 𝟏/𝟐 𝒙 𝟗𝟎 = 𝟒5

4. Tentukan pola ke-11 pada barisan bilangan ganjil ini!

Penyelesaian : 𝑼𝒏 = 𝟐 𝒙 𝒏 − 𝟏 = 𝟐𝒏 − 𝟏

𝑼𝟏𝟏 = 𝟐𝒙𝟏𝟏 − 𝟏 = 𝟐1

5. Tentukan pola ke-7 pada barisan bilangan genap tersebut !

Penyelesaian : 𝑼𝒏 = 𝟐 𝒙 𝒏 = 𝟐𝒏 𝑼𝟕 = 𝟐 𝒙 𝟕 = 𝟏4

6. Barisan bilangan 3, 7, 11, 15, 19, … Tentukan suku ke-10?

Penyelesaian :

𝑼𝟏 = 𝒂 = 𝟑 𝒃 = 𝟒

𝑼𝒏 = 𝒂𝒏 + 𝒃 —— 𝑼𝟏𝟎 = 𝟑. 𝟏𝟎 + 𝟒 = 𝟑4

7. Diberikan suatu pola bilangan 3, 5, 8, 12, 17, …, dua suku berikutnya dari pola

bilangan di atas adalah ….

Penyelesaian:

Untuk mendapatkan bilangan dua suku berikutnya hanya perlu melakukan dua kali perhitungan mengikuti pola yang diberikan. Seperti yang terlihat pada cara berikut:

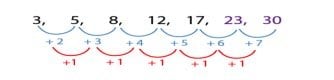
Jadi, dua suku berikutnya dari pola bilangan 3, 5, 8, 12, 17, … adalah 23 dan 30

8. Tentukan Suku ke-40 dari barisan aritmatika berikut 7, 5, 3, 1, …

Penyelesaian:

Diketahui : 𝑎 = 7 𝑑𝑎𝑛 𝑏 = −2

Ditanya : …..??

Jawab:

𝑼𝒏 = 𝑎 + (𝑛 − 1)𝑏

𝑈40 = 7 + (40 − 1)(−2)

= 7 + 39 (−2)

= 7 + (−78)

= −𝟕𝟏

9. Banyaknya suku dari barisan bilangan 6, 10, 14, … , 110, adalah ….

Penyelesaian:

Diketahui : 𝑎 = 6 𝑑𝑎𝑛 𝑏 = 10 − 6 = 4

Ditanya : 𝑛 =…..??

Jawab:

𝑼𝒏 = 𝑎 + (𝑛 − 1)𝑏

110 = 6 + (𝑛 − 1) 4

110 = 6 + 4𝑛 − 4

110 = 4𝑛 + 2

4𝑛 = 110 − 2

𝒏 = 𝟏𝟎𝟖/𝟒 = 𝟐7

10. Tentukan jumlah 10 suku pertama dari barisan aritmatika 3, 5, 7, 9, ….

Penyelesaian :

Pada barisan ini, 𝑈1 = 𝑎 = 3, 𝑑𝑎𝑛 𝑏 = 5 − 3 = 2

𝑼𝒏 = 𝑎 + (𝑛 − 1)𝑏

𝑼𝟏𝟎 = 3 + (10 − 1)2 = 3 + 9(2) = 3 + 18 = 21

Maka : 𝑆𝑛 = 𝑛/2 (𝑎 + 𝑈𝑛)

𝑆10 = 10/2 (3 + 𝑈10)

𝑆10 = 5(3 + 21) = 5 (24) = 𝟏𝟐0

11. Dalam sebuah aula terdapat 25 buah kursi pada baris pertama. Setiap baris berikutnya bertambah 3 kursi dari kursi di depannya. Jika aula itu memuat 8 baris kursi, tentukan banyak kursi dalam aula.

Penyelesaian :

Susunan kursi dalam aula membentuk deret aritmatika, dengan 𝑈1 = 25, 𝑑𝑎𝑛 𝑏 = 3 𝑑𝑎𝑛 𝑛 = 8.

Maka banyak kursi dalam aula tersebut :

𝑺𝒏 = 𝒏/𝟐 (𝟐𝒂 + (𝒏 − 𝟏) 𝒃)

𝑆8 = 8/2 (2 𝑥 25 + (8 − 1) 3)

𝑆8 = 4(50 + 21)

𝑆8 = 4 𝑥 71 = 𝟐𝟖𝟒

12. Tentukan suku ke-8 dari barisan geometri 3, - 6, 12, - 24, ….

Penyelesaian : 𝑎 = 3 𝑑𝑎𝑛 𝑟 = − 6/3 = −2

𝑼𝒏 = 𝒂𝒓 pangkat 𝒏−𝟏

𝑼𝟖 = 𝟑 𝒙 (– 𝟐) pangkat 𝟖−𝟏

𝑼𝟖 = 𝟑 𝒙 (−𝟐) pangkat 𝟕

𝑼𝟖 = 𝟑 𝒙 (−𝟏𝟐𝟖)

𝑼𝟖 = −𝟑𝟖4

13. Diketahui suatu barisan geometri 𝑼𝟏 = 𝟏𝟓 𝒅𝒂𝒏 𝑼𝟑 = 𝟏𝟑𝟓. Tentukan nilai suku ke-5 ..?

Penyelesaian:

𝑼𝒏 = 𝒂𝒓 pangkat 𝒏−𝟏

𝑼𝟏 ——— 𝑎 = 15

𝑼𝟑 ——— 𝑎𝑟2 = 135

Substitusikan 𝑎 = 15 ke dalam persamaan 𝑎𝑟 pangkat 2 = 135

𝑎𝑟 pangkat 2 = 135

15 𝑥 𝑟 pangkat 2 = 135

𝑟 pangkat 2 = 135/15 = 9

𝑟 = ±√9 = ± 3

𝑟 = 3 𝑎𝑡𝑎𝑢 𝑟 = −3

Maka : Untuk 𝑟 = 3 , 𝑼𝟓 = 𝑎𝑟4 = 15 𝑥 3 pangkat 4 = 15 𝑥 81 = 1.215

Untuk 𝑟 = −3 , 𝑼𝟓 = 𝑎𝑟4 = 15 𝑥 (−3) pangkat 4 = 15 𝑥 81 = 1.215

14. Diketahui deret geometri 6 + 12 + 24 + 48 + ⋯. Tentukan jumlah 10 suku pertama

deret tersebut..?

Penyelesaian:

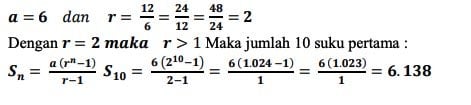
15. Dalam ruang rapat terdapat 20 kursi pada baris pertama, 22 kursi pada baris kedua dan 24 kursi pada baris ketiga. Jika dalam ruang rapat tersebut ada 10 baris, tentukanlah :

a. Banyaknya kursi pada baris paling belakang

b. Jumlah kursi dalam ruang rapat tersebut.

Penyelesaian: