tirto.id - Statistika menjadi salah satu materi penting yang dipelajari di kelas 12. Artikel ini akan membahas contoh-contoh soal statistika kelas 12 beserta pembahasannya, sehingga dapat membantu siswa lebih siap menghadapi ujian.
Statistika menjadi salah satu materi yang wajib dikuasai oleh siswa kelas 12 SMA. Siswa pun bisa belajar contoh-contoh soal agar bisa menghadapi ujian sekolah.
Statistika merupakan cabang dari pelajaran matematika yang berfokus pada pengumpulan, pengelompokan, serta menganalisis data sehingga dapat diambil suatu kesimpulan dari data yang disajikan.
Statistik SMA untuk kelas 12 akan terbagi dalam beberapa materi pembahasan. Siswa akan belajar mengenai pengukuran dan pengolahan data. Secara garis besar, materi statistik yang akan dipelajari oleh siswa kelas 12 meliputi:
A. Ukuran Pemusatan Data
- Mean: nilai rataan suatu data
- Median: nilai tengah dari suatu data
- Modus: nilai yang paling sering muncul atau memiliki frekuensi paling tinggi
- Datum: informasi berupa angka atau lambang yang apabila dikumpulkan akan menjadi data
- Kuartil: membagi kelompok data berurutan menjadi empat bagian yang sama
- Desil: data keseluruhan dibagi menjadi 10 bagian yang sama
- Jangkauan data: rentang data atau selisih dari datum terbesar dan terkecil
- Jangkauan antar kuartil: selisih antara kuartil ketiga dengan kuartil pertama (disebut juga dengan hamparan)
- Simpangan kuartil: setengah dari hamparan
- Simpangan rata-rata: ukuran seberapa jauh penyebaran nilai-nilai data terhadap nilai rataan
- Ragam: ukuran yang menyatakan rata-rata kuadrat jarak suatu data dari nilai rataannya
Pengumpulan data meliputi populasi sampel, sedangkan penyajian data digambarkan dalam bentuk tabel dan diagram (batang, lingkaran, grafik).
Contoh Soal Statistika Kelas 12 dan Pembahasan
Untuk bahan belajar di rumah, berikut kumpulan contoh soal statistika kelas 12 beserta jawaban dan pembahasannya:
1. Diketahui data berikut: 6, 4, 5, 8, 8, 4, 7, 6, 6. Nilai mean, median, dan modus berturut-turut adalah…
Jawaban:
Mean = (6 + 4 + 5 + 8 + 8 + 4 + 7 + 6 + 6) : 9 = 6
Median = (6 + 6) : 2 = 6
Modus = 6
2. Diketahui data sebagai berikut: 7, 5, 8, 6, 7, 8, 7, 7, 7, 9, 5, 8, 6, 8. Tentuan mean, median, modus, dan jangkauan datanya berturut-turut:
Jawaban:
Mean = (7 + 5 + 8 + 6 + 7 + 8 + 7 + 7 + 7 + 9 + 5 + 8 + 6 + 8) : 14 = 7
Median = (7+7) : 2 = 7
Modus = 7
Jangkauan data = 9 - 5 = 4
3. Diketahui data: 3, 7, 5, a, 6, 4, 6, 9, 6, 4
Jika rata-rata data tersebut adalah 6 maka nilai a…
Jawaban:
6 = (3 + 7 + 5 + a + 6 + 4 + 6 + 9 + 6 + 4) : 10
a = 10
4. Jika data 2, a, a, 3, 4, 6 mempunyai rataan c dan data 2, c, c, 4, 6, 2, 1 mempunyai rataan 2a, maka nilai c adalah…
Jawaban:
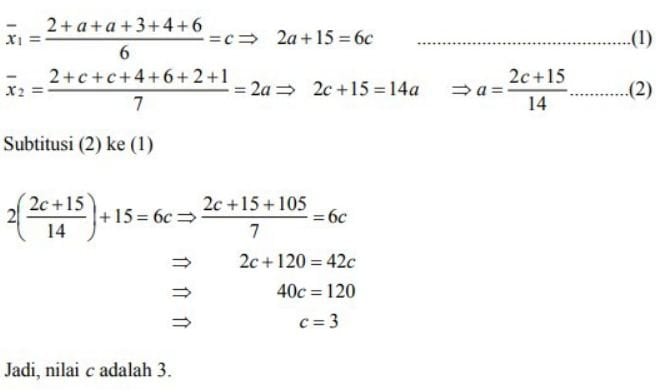
5. Rata-rata nilai ujian dari 40 siswa adalah 5,1. Jika seorang siswa tidak disertakan dalam perhitungan, maka rata-rata nilainya menjadi 5,0. Nilai siswa tersebut adalah…
Jawaban:

6. Nilai rata-rata ujian dari 43 siswa adalah 56. Jika nilai ujian 2 siswa, yaitu Toni dan Tono digabungkan, nilai rata-rata menjadi 55. Jika nilai Toni 25, berapakah nilai Tono?
Jawaban:

7. Suatu keluarga mempunyai 3 orang anak. anak termuda berumur x tahu. dua anak yang lain berumur x + 2 dan x + 7. Jika rata-rata hitung umur mereka adalah 24 tahun, maka anak termuda berumur…
Jawaban:
(x + (x + 2) + (x + 7)) : 3 = 24
3x + 9 = 24 . 3
3x = 72 - 9
x = 21
8. Rata-rata umur Guru dan Dokter adalah 40 tahun. Jika rata-rata umur guru adalah 35 dan rata-rata umur dokter adalah 50. Berapakah perbandingan banyak guru dan banyak dokter?
Jawaban:

9. Nilai rata-rata sekelompok siswa yang berjumlah 50 siswa adalah 64. Jika seorang siswa yang mendapat nilai 88,5 tidak dimasukkan dalam perhitungan rata-rata nilai sekelompok siswa, maka nilai rata-rata menjadi…
Jawaban:
Nilai total kelompok = 50 x 64 = 3200
Nilai rata-rata 49 siswa = (3200 - 88,5) : 49 = 63,5
10. Buatlah statistik terurut dan tentukan datum terkecil dan datum terbesarnya dari data berikut:12 32 45 21 25 16 17 30 33 15 35 38 40 12 23 14
Jawaban:
Statistik terurut: 12 12 14 15 16 17 21 23 25 30 32 33 35 38 40 45
Diperoleh ukuran data/banyaknya datum (n) = 16
Datum terkecil = X1 = Xmin = 12
Datum terbesar = Xn = Xmax = 45
11. Rataan bagi suatu kumpulan data yang terdiri dari sepuluh bilangan adalah 7. Apabila ditambah (1 + 3m) dan (1 + 5m) kepada kumpulan data itu, rataan menjadi 10. Tentukan nilai m!
Jawaban:

12. Angka-angka 8, 3, p, 3, 4, 10, q, 4, 12 memiliki mean = 6. Hitunglah nilai p + q, kemudian tentukan rata-rata p dan q!
Jawaban:
6 = (8 + 3 + p + 3 + 4 + 10 + q + 4 + 12) : 9
6 = (44 + p + q) : 9
54 = 44 + p + q
p + q = 54 - 44
p + q = 10
Rata-rata p dan q = 10 : 2 = 5
13. Diketahui data: 1 2 3 3 4 5 5 5 6 6 7 8 8 9 9 9 9
Tentukan kuartil bawah dan atas!
Jawaban:
Kuartil adalah nilai yang membagi data menjadi 4 bagian sama banyak. Q1 = kuartil bawah, Q2 = kuartil tengah, dan Q3 = kuartil atas

14. Diketahui data sebagai berikut: 1 2 2 2 3 3 4 4 5 5 5 6 6 7 8 8 9 9 9 9
Tentukan nilai desil ke-8!
Jawaban :
Desil adalah nilai yang membagi data menjadi 10 sama banyak. Ada 9 nilai desil dalam suatu data, yaitu D1 sampai D9.
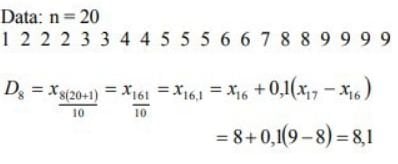
15. Jangkauan data: 6 8 2 2 3 9 5 4 5 5 4 6 1 7 8 2 9 3 9 9 adalah …
Jawaban:
J = Xn - X1 = Xmax - Xmin
Xn = datum terbesar
X1 = datum terkecil
Data terurut: 1 2 2 2 3 3 4 4 5 5 5 6 6 7 8 8 9 9 9 9J = X20 - X1 = 9 - 1 = 8
16. Carilah nilai Hamparan (H) dan Simpangan Kuartil (SK) untuk data: 1 2 3 3 4 5 5 5 6 6 7 8 8 9 9 9 9
Jawaban:
Untuk data tunggal: H = Q3 - Q1 dan Qd = ½ H
Dari data di atas, maka diperoleh:
Q1 = 3,5 dan Q3 = 7,25
H = 7,25 - 3,5 = 3,75
Qd = ½ x 3,75 = 1,88
17. Dari data pada soal no. 16, tentukanlah nilai langkah (L), pagar dalam (PD), dan pagar luar (PL). Jika ada, tentukanlah pencilannya.Jawaban:
Rumus:
L = 3/2 H = 3/2 (Q3 - Q1)
PD = Q1 - L
PL = Q3 + L
Biasa digunakan untuk melihat ada tidaknya pencilan dalam suatu data.
Dari data: 1 2 2 2 3 3 4 4 5 5 5 6 6 7 8 8 9 9 9 9, diperoleh:Q1 = 3,5
Q3 = 7,25
H = 3,75
Maka:L = 3/2 x 3,75 = 5,63
PD = 3,5 - 5,63 = -2,13
PL = 7,25 + 5,63 = 12,88
Datum yang kurang dari PD atau lebih dari PL disebut dengan pencilan. Untuk data di atas, diketahui tidak memiliki pencilan.
18. Tentukan ragam (R) dan simpangan baku (S) dari data berikut: 1 2 3 4 5
Jawaban:

19. Suatu data memiliki simpangan baku S = √2 . Jika masing-masing datum dikalikan 3 kemudian dikurangi 5, maka simpangan baku menjadi…
Jawaban:
Jika suatu data, setiap datumnya dikalikan dengan a dan ditambah b, maka simpangan baku baru (Sb):
Sb = |a| . S
Jadi, Sb = |3| . S = 3√2
20. Tentukan statistik 5 serangkai dari data berikut: 7 5 10 20 13 8
Jawaban:
Statistik 5 serangkai adalah: X1, Xn, Q1, Q2, Q3
Data terurut: 2 5 7 8 10 13 20
Maka:
X1 = 2
Xn = 20
Q1 = 5
Q2 = 8
Q3 = 13.
Penulis: Erika Erilia
Editor: Yulaika Ramadhani












