tirto.id - Bocoran soal UTBK SNBT menjadi salah satu hal berharga yang dapat dimanfaatkan peserta untuk mempersiapkan diri. Salah satu materi dalam UTBK SNBT yang mulai digelar 30 April 2024 lalu adalah pengetahuan kuantitatif.
Pengetahuan kuantitatif masih masuk sebagai materi dalam Ujian Tulis Berbasis Komputer (UTBK) dalam Seleksi Nasional Berdasarkan Tes (SNBT). SNBT sendiri merupakan salah satu jalur masuk ke perguruan tinggi negeri.
Pelaksanaan UTBK SNBT 2024 dibagi ke dalam 2 gelombang. UTBK SNBT 2024 Gelombang 1 dilaksanakan mulai 30 April hingga 7 Mei 2024 mendatang.
Akan tetapi, perlu dicatat, bahwa tidak ada penyelenggaraan UTBK pada 1 Mei 2024 karena merupakan tanggal merah. Sementara itu, UTBK SNBT Gelombang 2 dijadwalkan pada 14-20 Mei 2024.
Kisi-Kisi Soal UTBK Pengetahuan Kuantitatif
Dalam UTBK SNBT 2024, peserta akan menghadapi dua jenis tes, meliputi skolastik dan literasi. Salah satu jenis materi yang diujikan dalam Tes Skolastik adalah Pengetahuan Kuantitatif (PK).
Pengetahuan Kuantitatif adalah materi ujian yang digunakan untuk mengukur tingkat pengetahuan peserta dalam hal matematika. Pengetahuan Kuantitatif diperoleh peserta dari pembelajaran dan kemampuan untuk menggunakan informasi kuantitatif serta memanipulasi simbol-simbol angka.
Dalam UTBK SNBT 2024, materi Pengetahuan Kuantitatif adalah sebagai berikut:
- Ukuran perhitungan matematika
- Pemecahan masalah matematika
- Pengetahuan umum matematika.
Kumpulan Bocoran Soal UTBK SNBT 2024 Pengetahuan Kuantitatif dan Jawabannya
Mengerjakan soal menjadi salah cara terbaik yang dapat dilakukan peserta dalam menghadapi UTBK SNBT 2024. Berikut ini bocoran soal UTBK SNBT 2024 materi Pengetahuan Kuantitatif dan jawabannya:
1. Diketahui X₁ dan X₂ adalah akar-akar dari persamaan x² + 3aX - (9+a) = 0. Apabila X₁² ditambah X₂² hasilnya 29, berapa nilai a dengan a lebih 0...
A. 5
B. 4
C. 3
D. 2
E. 1
Jawaban: E. 1
2. Perhatikan pernyataan berikut.
(1) f(3x)=3+6x
(2) f(2) > 7
(3) f(0) = 5
(4) g-1(-2)=-7
Apabila diketahui rumus fungsi (gof)(x-1) = x + 2 dan f(x) = 2x + 3. Manakah pernyataan yang benar?
A. (1) dan (2)
B. (1) dan (3)
C. (1) dan (4)
D. (2), dan (3)
E. (2) dan (4)
Jawaban: C. (1) dan (4)
3. Sebuah persamaan kuadrat Y = 3x² + (m − 2)x + 3 diketahui memiliki akar-akar kembar dan m > 0. Berapa nilai m yang memenuhi dari persamaan kuadrat tersebut?
A. 4
B. 2
C. 3
D. 6
E. 8
Jawaban: E. 8
4. Perhatikan pernyataan berikut.
(1) U3 > 8
(2) Suku pertama adalah 3
(3) U7 = 26
Apabila diketahui suatu barisan aritmatika x -2, 6, 2x + 2, 14,... Manakah pernyataan yang benar...
A. (1) dan (2)
B. (1) dan (3)
C. (2) dan (3)
D. (2)
E. (1), (2), dan (3)
Jawaban: B. (1) dan (3)
5. Diketahui rumus fungsi f(x) = 2x − 3 dan (g o f)(x) = 4x – 9. Berapa nilai g-1 apabila mengacu kedua rumus fungsi tersebut...
A. 0
B. 1
C. -1
D. 2
E. -2
Jawaban: B. 1
6. Diketahui (fog)(x) = 4x-2 dan g(x) = 2x+5. Berapa nilai dari invers F(x)...
A. 2x-10
B. 2x-12
C. 2x+12
D. (x+12)/2
E. (x-12)/2
Jawaban: E. (x-12)/2
7. Diketahui F(x) = (2x+3)^1/3 – 2. Tentukan Invers dari F(x)....
A. 1/2 (x+2)³-3/2
B. 1/2 (x-2)³+3/2
C. 1/3 (x+2)³-3/2
D. 1/3 (x-2)³+3/2
E. (x+2)³-3/2
Jawaban: A. 1/2 (x+2)³-3/2
8. Diketahui rumus fungsi F(x) = (5x-1)/(2x+3). Tentukan invers dari F(x)...
A. 3x+1/2x-5
B. -3x+1/2x-5
C. 3x+1/2x+5
D. 3x-1/2x-5
E. -3x-1/2x-5
Jawaban: E. -3x-1/2x-5
9. ²log (3x-1) = 3. Berapa nilai dari x...
A. 2
B. 3
C. 4
D. 5
E. 6
Jawaban: B. 3
10. 4^x+3 = ³√8^x+3. Nilai x adalah....
A. -2
B. -3
C. -4
D. 2
E. 3
Jawaban: B. -3
11. Segitiga ABC siku-siku dengan P = a dan Q = 80
A. Tidak dapat ditentukan hubungan P dan Q
B. Q>P
C. P=Q
D. P>Q
Jawaban: A. Tidak dapat ditentukan hubungan P dan Q
12. Diketahui tiga bilangan asli berbeda dan kurang dari 10 dipilih sekaligus secara acak. Lantas, dari empat pernyataan berikut, berapakah yang bernilai benar berdasarkan informasi di atas?
(1) Peluang semua bilangan yang terpilih prima kurang dari 1/20
(2) Peluang semua bilangan yang terpilih genap kurang dari 1/25
(3) Peluang jumlah semua bilangan yang terpilih kurang dari 8 adalah 1/42
(4) Peluang semua bilangan yang terpilih ganjil lebih dari 1/7
A. 0
B. 1
C. 2
D. 3
E. 4
Jawaban: E. 4
13. Perhatikan barisan bilangan real 2, a, 8, ...
Apakah 16 adalah salah satu suku barisan di atas?
Untuk menjawab pertanyaan tersebut, putuskan apakah pernyataan (1) dan (2) berikut ini sudah cukup sebagai jawaban:
(1) Barisan tersebut adalah barisan aritmetika
(2) Barisan tersebut adalah barisan bilangan positif
A. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetap pernyataan (2) SAJA tidak cukup
B. Pernyataan (1) dan (2) cukup untuk menjawab pertanyaan, tetapi salah satu keduanya tidak cukup
C. Pernyataan (1) ataupun pernyataan (2) SAJA sudah cukup untuk menjawab pertanyaan
D. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan
E. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup
Jawaban: E. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup
Gambar di bawah ini untuk soal nomor 14 dan 15!
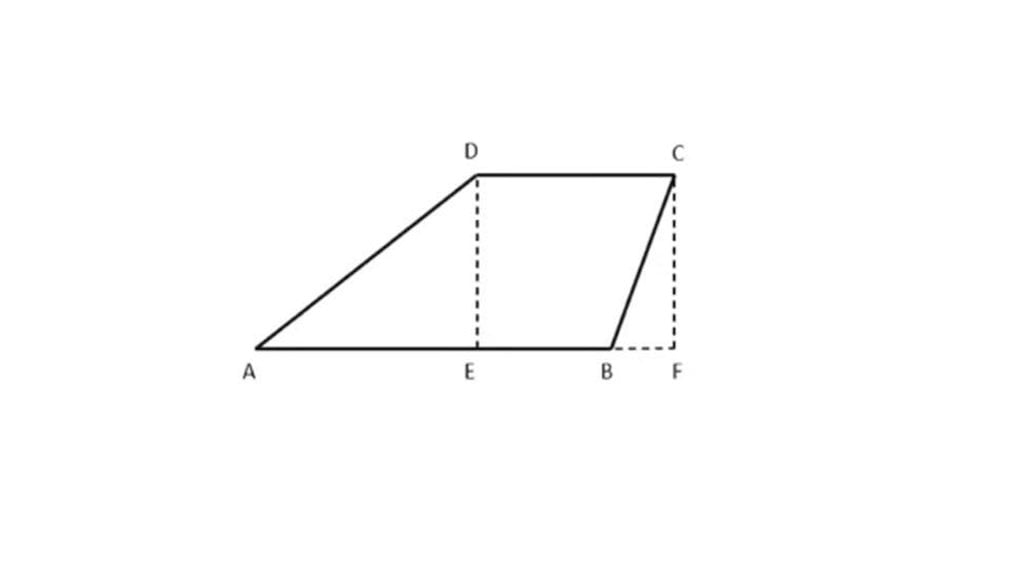
14. Pada trapesium ABCD dengan AB || CD, titik E dan F terletak pada garis AB sehingga DE tegak lurus AB dengan CF || DE. Maka, sudut ADC = ......
A. 100°
B. 135°
C. 105°
D. 120°
E. 145°
Jawaban: B. 135°
15. AE = ...
A. 2√3
B. 2√2
C. √2
D. 3
E. √3
Jawaban: A. 2√3
Penulis: Syamsul Dwi Maarif
Editor: Ahmad Yasin & Yulaika Ramadhani