Contoh Soal Program Linier Kelas 11 Semester 1 dan Jawabannya

tirto.id - Program linier merupakan salah satu materi yang terdapat dalam mata pelajaran matematika kelas 11 semester 1. Berbagai contoh soal mengenai materi program linier kelas 11 dapat dimanfaatkan oleh para siswa sebagai bahan belajar untuk mempersiapkan diri dalam menghadapi ulangan harian atau ujian semester yang akan datang.

Tanpa disadari dalam kehidupan sehari-hari kita selalu melibatkan prinsip-prinsip program linier diantaranya seperti pemakaian tanah untuk lahan parkir, menghitung keuntungan maksimum suatu usaha, pengeluaran minimum yang dibelanjakan,serta penggunaan prinsip program linier pada proyek bangunan perumahan.

Program linier terdiri atas persamaan-persamaan linier dan pertidaksamaan linier. Program linier itu sendiri didefinisikan sebagai suatu metode yang digunakan untuk menentukan besarnya masing-masing nilai optimum (maksimum atau minimum) dari suatu persoalan linier. Nilai optimum tersebut diperoleh dari nilai yang terdapat dalam suatu himpunan penyelesaian persoalan linier.

Dilansir e-Modul Matematika kelas 11 yang diterbitkan oleh Kementerian Pendidikan dan Kebudayaan, dalam materi program linier terdapat beberapa topik yang akan menjadi pokok pembahasan mulai dari Pengertian Program Linier, Sistem Pertidaksamaan Linier Dua Variabel, Daerah Penyelesaian Suatu Pertidaksamaan Linier Dua Variabel, Fungsi Tujuan dan Fungsi Kendala dari Program Linier, serta Nilai Optimum Fungsi Objektif.

Contoh Soal Program Linier Kelas 11 dan Jawaban

Berikut ini disajikan beberapa contoh soal program linier beserta jawabannya yang dapat dipelajari oleh siswa untuk memperdalam pemahaman mengenai materi program linier dalam mata pelajaran matematika kelas 11 semester 1:

1. Seorang tukang las membuat dua jenis pagar. Tiap meter persegi jenis 1 memerlukan 4 meter besi pipa dan 6 meter besi beton. Adapun pagar jenis 2 memerlukan 8 meter besi pipa dan 4 meter besi beton. Tukang las tersebut mempunyai persediaan 640 meter besi pipa dan 480 meter besi beton. Harga jual per meter persegi jenis 1 Rp50.000,- dan harga jual per meter persegi pagar jenis 2 adalah Rp 75.000,-. Buatlah model matematika dari permasalahan Linier tersebut agar hasil penjualannya mencapai nilai maksimum!

Jawaban:

Misalkan: x = banyaknya pagar jenis 1 y = banyaknya pagar jenis 2 fungsi Obyektif f(x,y) = 50.000x + 75.000y

Kendala/Syarat: i. 4𝑥 + 8𝑦 ≤ 640 (kedua ruas dibagi dengan 4) 𝑥 + 2𝑦 ≤ 160 ii. 6𝑥 + 4𝑦 ≤ 480 (kedua ruas dibagi 2) 3𝑥 + 2𝑦 ≤ 240 iii. 𝑥 ≥ 0 iv. 𝑦 ≥0

2. Seorang pedagang sepatu merencanakan akan membeli tidak lebih dari 100 pasang sepatu wanita dan pria untuk di jual. Harga beli sepasang sepatu pria Rp 20.000 dan sepasang sepatu wanita Rp.30.000. Modal yang tersedia Rp.2.400.000. Keuntungan untuk sepasang sepatu pria Rp. 4.000 dan sepasang sepatu wanita Rp. 5.000. Buatlah model matematikanya!

Jawaban:

Model Matematika

Misal:

Sepatu pria = x

Sepatu wanita = y

Model matematikanya Bentuk objektif: F(x,y) = 4.000x + 5.000y

Kendala/Syarat :

x + y ≤100..............................................................................................(i)

20.000x + 300.000y ≤ 2.400.000(kedua ruas dibagi dengan 10.000)

2x + 3y ≤ 240…....................................................................................(ii)

x ≥ 0…......................................................................................................(iii)

y ≥ 0…......................................................................................................(iv)

3. Seorang pemborong akan membangun rumah di atas tanah seluas 10.000 m2. Rumah yang akan dibangun terdiri dari dua tipe yaitu RS dan RSS. Luas tanah tipe RS 100 m2 dan luas tanah tipe RSS 80 m2. Sebuah rumah tipe RS dikerjakan oleh 5 orang dan sebuah rumah tipe RSS dikerjakan oleh 3 orang, sedangkan tenaga kerja yang tersedia 450 orang. Rumah itu akan dijual dengan keuntungan Rp 1.000.000 untuk satu unit RS dan Rp 750.000 untuk satu unit RSS. Buat model matematika dan tulis labanya dalam x dan y!

Jawaban:

Misal:

Rumah Tipe RS = x

Rumah Tipe RSS = y

Syarat/Kendala :

100 x + 80 y ≤ 10.000 (Kedua ruas dibagi dengan 20)

5x + 4y ≤ 500

5x + 3y ≤ 450

x ≥ 0 (Karena tidak mungkin sebuah type rumah bernilai negatif)

y ≥ 0 (Karena tidak mungkin sebuah type rumah bernilai negatif)

Labanya: 1.000.000 x + 750.000 y (dijadikan sebagai fungsi tujuan atau fungsi objektif), sehingga f(x,y) = 1.000.000x + 750.000y

4. Seorang siswa dapat memilih jurusan IPA, jika memenuhi syarat sebagai berikut:

i). Nilai matematika lebih dari 6

ii). Nilai fisika minimal 7

iii). Jumlah nilai matematika dan fisika tidak boleh kurang dari 13

Buat model matematika sebagai syarat seorang siswa bisa ke jurusan IPA

Jawaban:

Misal: Matematika = x dan Fisika = y

Maka Model Matematika adalah dijadikan sebagai Syarat atau Kendalanya, yaitu:

i). x > 6

ii). y ≥ 7

iii). x + y ≥ 13 dengan x, y ϵ R

5. Tentukan nilai minimum dari 3x + 2y dari sistem pertidaksamaan: x + 2y ≥ 6 ; 2x + y ≥ 6 ; x ≥ 0 ; y ≥ 0, untuk x ,y ∊ R

Jawaban :

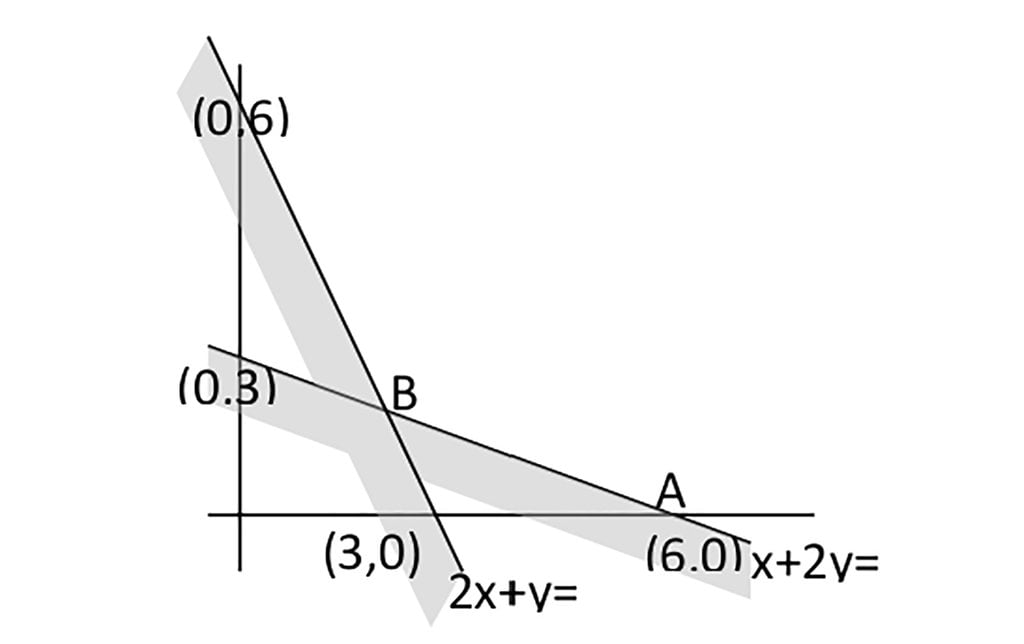
Titik-titik sudut daerah Himpunan Penyelesaiannya adalah: Titik A (6,0), titik C (0,6) dan titik B yang diperoleh dari titik potong garis x + 2y ≥ 6 dan 2x + y ≥ 6.

Untuk menentukan titik B kalian gunakan metode eliminasi dan substitusi

x + 2y = 6 (dikali 1)

2x + y = 6 (dikali 2)

Sehingga diperoleh :

x + 2y = 6

4x + 2y =12

Kemudian dieliminasi hasilnya menjadi 3x = 6, maka nilai x = 2

substitusi nilai x = 2 ke persamaan x + 2y = 6 sehingga diperoleh 2 + 2y = 6. Nilai y adalah

2y = 6-2

2y = 4

y = 2

jadi titik B adalah (2 , 2) untuk memperoleh nilai minimum, harus kalian uji titik-titik sudut tersebut ke fungsi obyektif f(x,y) = 3x + 2y, sehingga diperoleh

titik A (6,0) nilai fungsi obyektif f(6,0)= 3(6)+2(0)= 18 + 0 = 18.

titik B (2,2) nilai fungsi obyektif f(220)= 3(2)+2(2)= 6 + 4 = 10.

titik C (0,6) nilai fungsi obyektif f(0,6)= 3(0)+2(6)= 0 + 12 = 12.

berdasarkan hasil uji titik tersebut maka kalian akan melihat nilai yang paling minimum adalah 10 yang diperoleh dari x = 2 dan y = 2

6. Tentukan sistem pertidaksamaan dari daerah himpunan penyelesaian berikut: (daerah Himpunan Penyelesaian adalah daerah yang bersih).

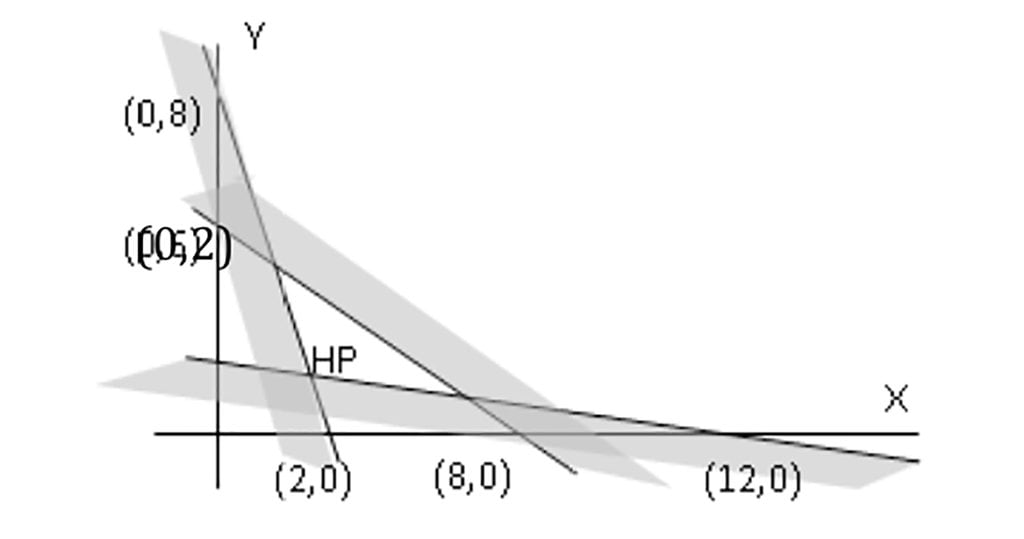
Jawaban Alternatif :

i.Pertidaksamaan untuk (2,0) dan (0,8)

8𝑥 + 2𝑦 ≥ 16 (kedua ruas dibagi dengan 2)

4𝑥 + 𝑦 ≥ 8

ii. Pertidaksamaan untuk (8,0) dan (0,6)

6𝑥 + 8≤ 48 (kedua ruas dibagi dengan 2)

3𝑥 + 4≤ 24

iii. Pertidaksamaan untuk titik (12,0) dan (0,2)

2𝑥 + 12𝑦 ≥ 24 (kedua ruas dibagi dengan 2)

𝑥 + 6𝑦 ≥ 12

Sehingga pertidaksamaan pada grafik di atas adalah 4𝑥 + 𝑦 ≥ 8; 3𝑥 + 4≤ 24; 𝑥 + 6𝑦 ≥ 12; 𝑥 ≥ 0, y ≥ 0, Untuk x, y ∈ R.

7. Tentukan nilai maksimum dari 2x + 3y, x , y ϵ C yang memenuhi sistem pertidaksamaan x + y ≤ 3 ; x + 2y ≤ 4, x ≥ 0; y ≥ 0

Jawaban :

Terlebih dahulu digambar daerah Himpunan Penyelesaian dari sistem pertidaksamaan di atas. Kemudian dihitung nilai 2x+3y pada setiap titik dalam daerah himpunan penyelesaian.

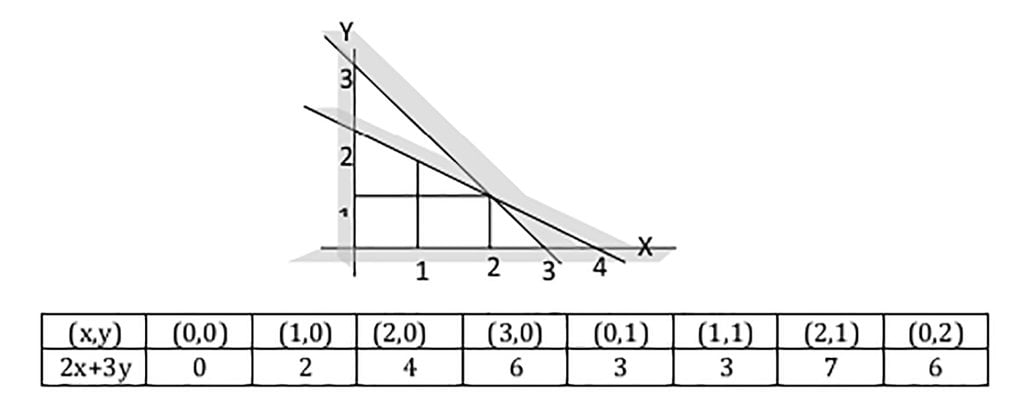
Berdasarkan tabel di atas, maka nilai maksimum dari 2x + 3y adalah 7 untuk x = 2 dan y = 1. Nilai maksimum diperoleh pada titik sudut daerah himpunan penyelesaian, berdasarkan nilai tersebut, maka untuk menentukan nilai optimum suatu bentuk objektif f(x,y) = ax + by, kalian cukup menghitung nilai pada tiap titik-titik sudut atau titik yang dekat dengan titik sudut pada daerah himpunan penyelesaian.

8. Tentukan nilai maksimum dari 2x + 3y, x, y ϵ R. yang memenuhi sistem pertidaksamaan x + y ≤ 3, x + 2y ≤4, x ≥ 0, y ≥ 0 dengan garis selidik!

Jawaban :

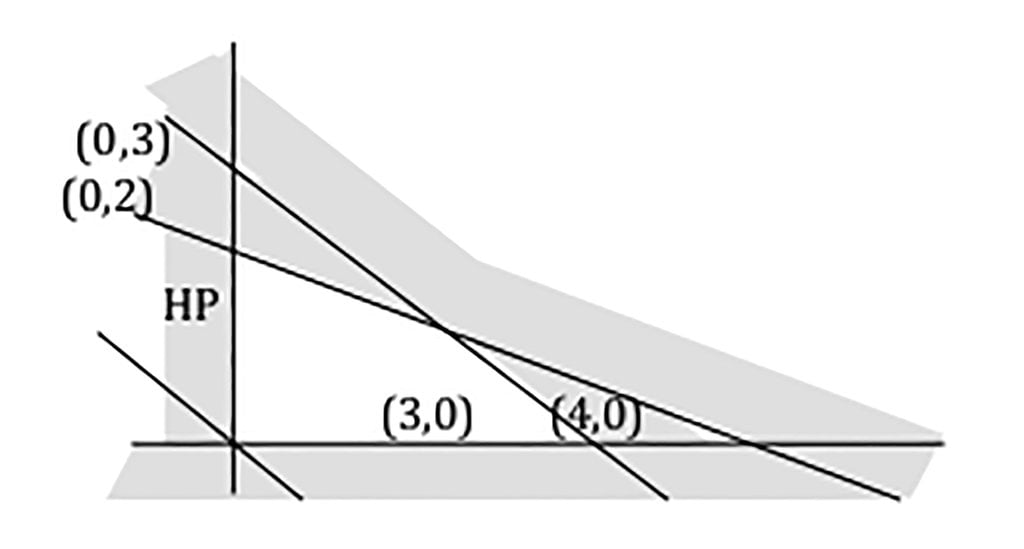
Buat garis 2x + 3y = 0, kemudian dibuat garis-garis yang sejajar dengan garis 2x + 3y = 0 yang melalui setiap titik-titik sudut yaitu 2x + 3y = 6 dan 2x + 3y = 7. Titik sudut yang paling kanan (terakhir) disentuh oleh garis selidik adalah merupakan nilai optimum. Sehingga nilai maksimumnya = 7 untuk x = 2 dan y = 1.

9. Perhatikan gambar grafik di bawah ini:

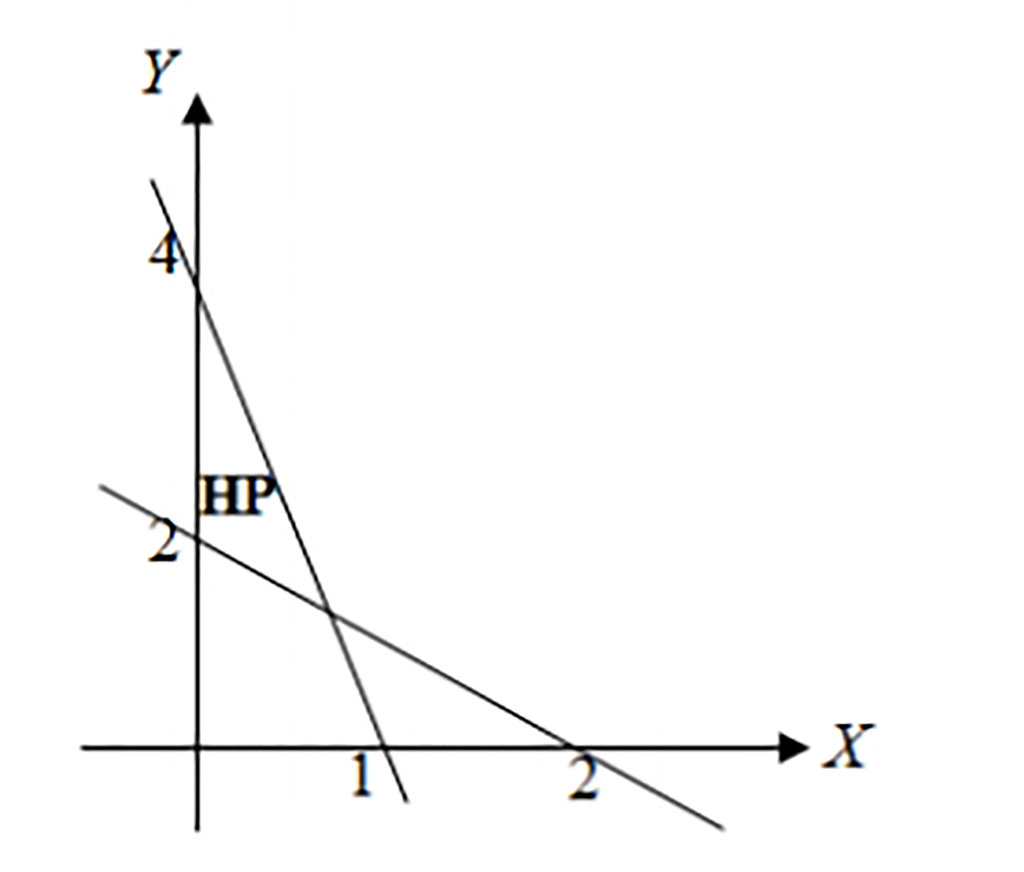
Jawaban :

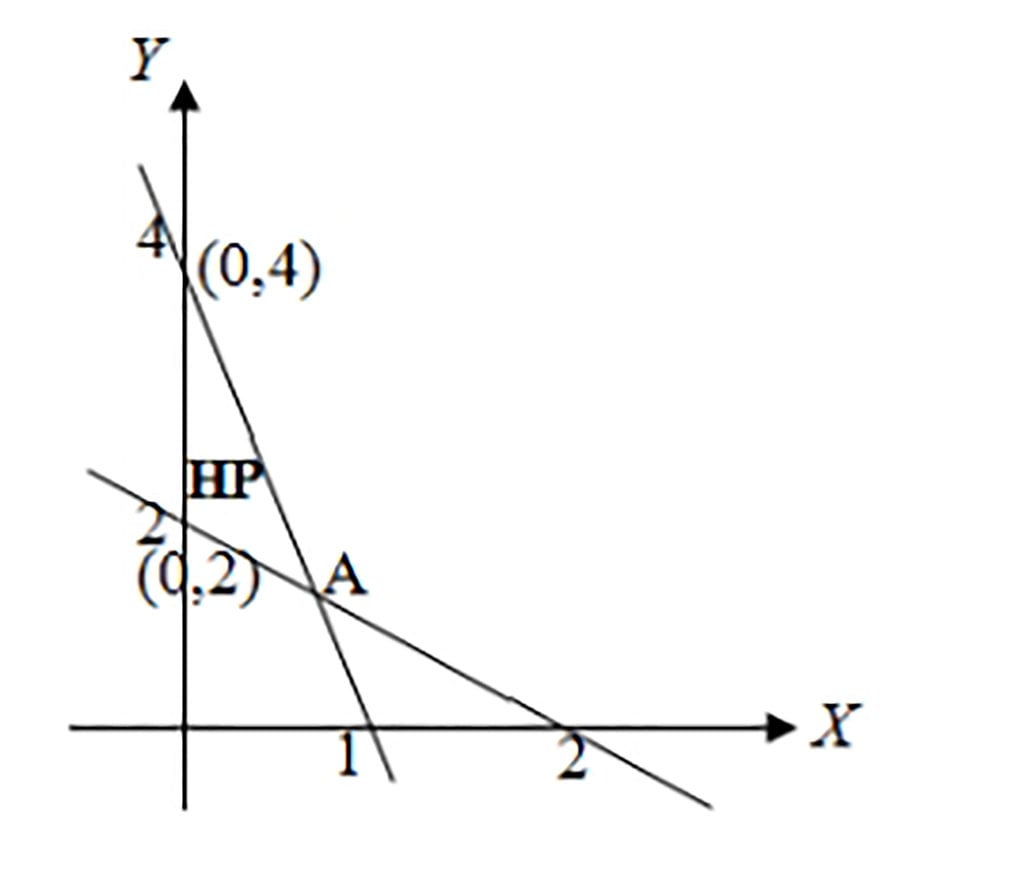
Terlebih dahulu cari titik A:

4𝑥 + ≤ 4 ………………….(1)

𝑥 + 𝑦 ≥ 2 …………………... (2)

Titik A merupakan titik potong antara garis 4x + y = 4 dengan garis x = y = 2, dengan menggunakan metode gabungan, akan diperoleh:

Dengan metode eliminasi

4x + y = 4

x + y = 2

Hasilnya :

3x = 2

x = 2/3

substitusi nilai x = 2/3 ke persamaan 4x + y = 4, sehingga

4x + y = 4

4(2/3) + y = 4

8/3 + y = 4

y = 4 – 8/3

y = 12/3 – 8/3

y = 4/3

jadi titik potongnya (2/3 , 4/3)

selanjutnya kalian tentukan nilai minimum dari fungsi obyektif f(x,y) = 5x + 3y

titik (0,2) maka f(0,2) = 5(0) + 3(2) = 0 + 6 = 6

titik (2,0) maka f(2,0) = 5(2) + 3(0) = 10 + 0 = 10

titik (2/3 , 4/3) maka f(2/3 , 4/3)= 5(2/3) + 3(4/3) = 10/3 + 12/3 = 22/3

dari hasil uji titik di atas maka akan kalian lihat nilai minimumnya yaitu 6

10. Bentuk pertidaksamaan dari grafik di bawah ini yaitu ...

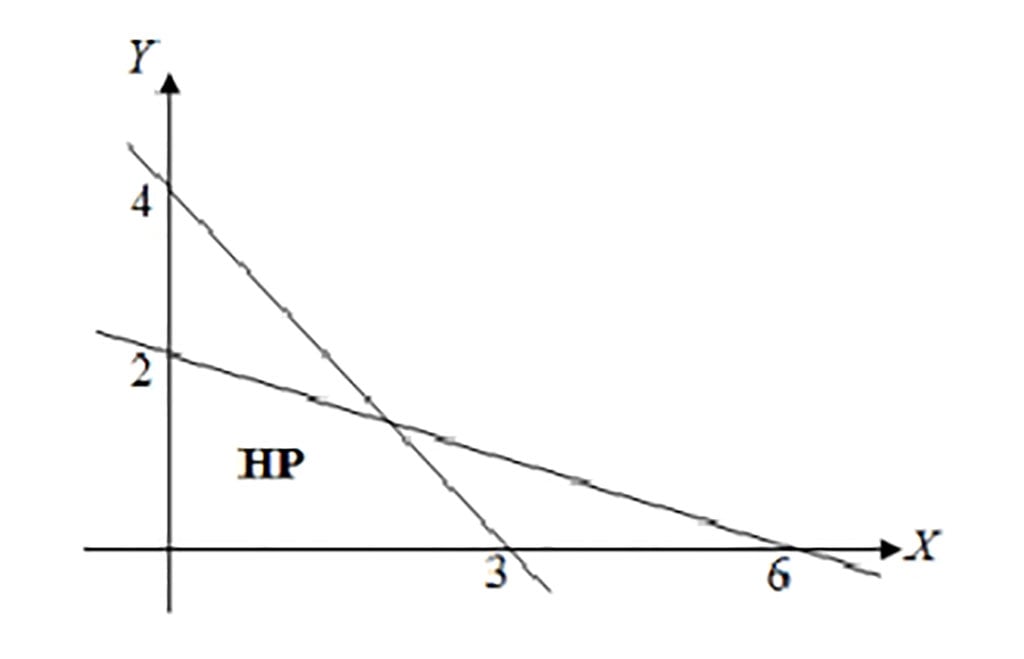
Jawaban :

Persamaan garis ke 1, Lihat tabel titik bantu berikut :

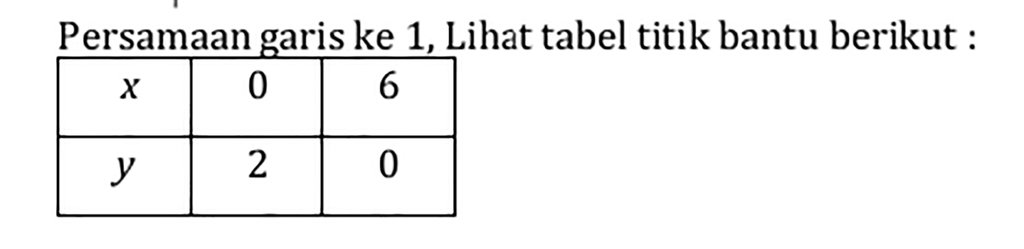
Persamaan garisnya adalah 2x + 6y = 12 (Kedua ruas dibagi dengan 2) sehingga x + 3y = 6

Untuk menentukan Daerah Himpunan Penyelesaiannya Uji salah satu titik yang tidak terletak pada garis x + 3y = 6

Misal titik (0,0) → artinya nilai x = 0 dan y = 0, substitusi ke 𝑥 + 3𝑦 ≤ 6, sehingga 0 + 3(0) ≤ 6 atau 0+0 ≤ 6 (Benar), maka daerah Himpunan Penyelesaiannya Di bawah garis x+ 3y = 6

Persamaan garis ke 2, Lihat tabel titik bantu berikut:

Persamaan garisnya adalah 4x + 3y = 12, Untuk menentukan Daerah Himpunan Penyelesaiannya Uji salah satu titik yang tidak terletak pada garis 4x + 3y = 12,

Misal titik (0,0) → artinya nilai x = 0 dan y = 0, substitusi ke 4𝑥 + 3𝑦 ≤ 12, sehingga 4(0) +3(0) ≤ 12 atau 0+0 ≤ 12 (Benar), maka daerah Himpunan Penyelesaiannya Di bawah garis 4x + 3y = 12

Persamaan garis ke 3 adalah 𝑥 ≥ 0

Persamaan garis ke 4 adalah y ≥ 0

Sehingga sistem pertidaksamaannya adalah 4𝑥 + 3𝑦 ≤ 12; 𝑥 + 3𝑦 ≤ 6; ≥ 0; 𝑦 ≥ 0